练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在正方体 中， 分别为 的中点，点 是底面内一点，且 平面 ，则 的最大值是( )

    A. B. 2 C. D.

    【答案】C

    【解析】分析：连结AC、BD，交于点O，连结A1C1，交EF于M，连结OM，则AOPM，从而A1P=C1M，由此能求出tan∠APA1的最大值．

    详解：连结AC、BD，交于点O，连结A1C1，交EF于M，连结OM，

    设正方形ABCD﹣A1B1C1D1中棱长为1，

    ∵在正方形ABCD﹣A1B1C1D1中，E，F分别为B1C1，C1D1的中点，

    点P是底面A1B1C1D1内一点，且AP∥平面EFDB，

    ∴AOPM，∴A1P=C1M=，

    ∴tan∠APA1===2．

    ∴tan∠APA1的最大值是2．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知非零数列满足，.

    （1）求证：数列是等比数列；

    （2）若关于的不等式有解，求整数的最小值；

    （3）在数列中，是否存在首项、第项、第项()，使得这三项依次构成等差数列？若存在，求出所有的；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C：x2+y2﹣4x+3＝0，过原点的直线l与圆C有公共点．

    （1）求直线l斜率k的取值范围；

    （2）已知O为坐标原点，点P为圆C上的任意一点，求线段OP的中点M的轨迹方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知m、n是不重合的直线，α、β是不重合的平面，有下列命题：①若mα，n∥α，则m∥n；②若m∥α，m∥β，则α∥β；③若α∩β=n，m∥n，则m∥α且m∥β；④若m⊥α，m⊥β，则α∥β.其中真命题的个数是（ ）

    A. 0B. 1C. 2D. 3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为是椭圆的两个焦点，是椭圆上任意一点，且的周长是6.

    （1）求椭圆的方程；

    （2）设圆：，过椭圆的上顶点作圆的两条切线交椭圆于两点，当圆心在轴上移动且时，求的斜率的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在某次诗词大会决赛前，甲、乙、丙丁四位选手有机会问鼎冠军，三名诗词爱好者依据选手在之前比赛中的表现，结合自己的判断，对本场比赛的冠军进行了如下猜测：猜测冠军是乙或丁；猜测冠军一定不是丙和丁；猜测冠军是甲或乙。比赛结束后发现，三个人中只有一个人的猜测是正确的，则冠军是（ ）

    A. 甲B. 乙C. 丙D. 丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数。

    （1）若函数的一个极值点为，求的单调区间；

    （2）若，且关于的不等式恒成立，求实数的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，，若，则

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】图甲中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律、对捕食者和被捕食者数量之间的关系描述错误的是（ ）

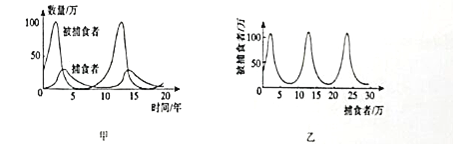
    A. 捕食者和被捕食者数量与时间以年为周期

    B. 由图可知，当捕食者数量增多的过程中，被捕食者数量先增多后减少

    C. 捕食者和被捕食者数量之间的关系可以用图1乙描述

    D. 捕食者的数量在第年和年之间数量在急速减少

    查看答案和解析>>

    同步练习册答案