
分析 由题意和等比数列的通项公式和求和公式可得首项和公比的方程组,解方程组代入求和公式可得.
解答 解:∵等比数列{an}的公比q<1,前n项和为Sn,且α3=2,S4=5S2,
∴α3=a1q2=2,S4=$\frac{{a}_{1}(1-{q}^{4})}{1-q}$=5S2=5×$\frac{{a}_{1}(1-{q}^{2})}{1-q}$,
联立解得a1=$\frac{1}{2}$,q=-2,
∴Sn=$\frac{\frac{1}{2}×[1-(-2)^{n}]}{1-(-2)}$=$\frac{1-(-2)^{n}}{6}$,
故答案为:$\frac{1-(-2)^{n}}{6}$.
点评 本题考查等比数列的求和公式,求出数列的首项和公比是解决问题的关键,属基础题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x-2015)一定是奇函数 | B. | f(x-2015)一定是偶函数 | ||
| C. | f(x+2015)一定是奇函数 | D. | f(x+2015)一定是偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | arcsin$\frac{4}{5}$ | B. | arcsin(-$\frac{4}{5}$) | C. | $\frac{π}{2}$+arcsin$\frac{4}{5}$ | D. | $\frac{π}{2}$+arccos$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
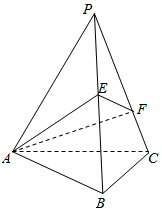 如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.
如图,已知正三棱锥P-ABC的底面边长为4,侧棱长为8,E、F分别为PB、PC上的动点,求截面△AEF周长的最小值,并求出此时三棱锥P-AEF的体积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com