
分析 列出函数关系式,利用基本不等式判断求解,注意定义域的求解.
解答 解:根据题意得出:y总利润=x(150-$\frac{3x}{2}$)-(600-72x)=$-\frac{3}{2}$x2-600+78x,
150$-\frac{3x}{2}$≥90,0<x≤40,
y平均利润=$-\frac{3x}{2}$$-\frac{600}{x}$+78,
∵$\frac{3x}{2}$$+\frac{600}{x}$≥2$\sqrt{900}$=60,(x=20时等号成立)
∴最大平均利润是-60+78=18(万元)
∴月生产20套时,每套设备的平均利润最大,最大平均利润是18万元
点评 本题考查了函数在解决最值问题中的应用,关键列出函数关系式,根据式子得出解决方法.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
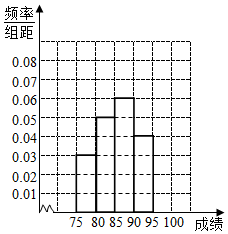 将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.
将某校高三年级300名学生的毕业会考数学成绩进行整理后,分成五组,第-组[75,80),第二组[80,85),第三组[86,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com