
| A. | y=$\frac{1}{{5}^{2-x}-1}$ | B. | y=($\frac{1}{2}$)1-2x | C. | y=$\sqrt{(\frac{1}{2})^{x}-1}$ | D. | y=$\sqrt{1-{2}^{x}}$ |
分析 依次对各项进行求解值域,根据题意选择不同的求法.
解答 解:对于A:y=$\frac{1}{{5}^{2-x}-1}$,∵52-x>0,∴52-x-1>-1且52-x-1≠0,∴y∈(-1,1),故A不对.
对于B:y=($\frac{1}{2}$)1-2x,∵1-2x∈R,∴y∈(0,+∞),故B对.
对于C:y=$\sqrt{(\frac{1}{2})^{x}-1}$,∵$(\frac{1}{2})^{x}=1$时,y=0,∴y∈[0,+∞),故C不对.
对于D:$y=\sqrt{1-{2}^{x}}$,∵2x>0,0≤1-2x<1,∴y∈[0,1),故D不对.
故选:B.
点评 本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
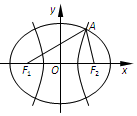 如图,F1,F2是双曲线C1:x2-$\frac{y^2}{3}$=1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点,若|F1F2|=|F1A|,则C2的离心率是( )
如图,F1,F2是双曲线C1:x2-$\frac{y^2}{3}$=1与椭圆C2的公共焦点,点A是C1,C2在第一象限的公共点,若|F1F2|=|F1A|,则C2的离心率是( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com