
已知椭圆C经过点A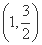 ,两个焦点分别为(-1,0),(1,0).
,两个焦点分别为(-1,0),(1,0).
(1) 求椭圆C的方程;
(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.
科目:高中数学 来源: 题型:
在极坐标系中,圆C1的方程为ρ=4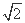 cos
cos ,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为
,以极点为坐标原点、极轴为x轴的正半轴建立平面直角坐标系,圆C2的参数方程为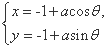 (θ是参数),若圆C1与圆C2相切,求实数a的值.
(θ是参数),若圆C1与圆C2相切,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
检测部门决定对某市学校教室的空气质量进行检测,空气质量分为A、B、C三级.每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格.设各教室的空气质量相互独立,且每次检测的结果也相互独立.根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为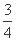 ,
, ,
, .
.
(1) 在该市的教室中任取一间,估计该间教室空气质量合格的概率;
(2) 如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为X,并以空气质量为A级的频率作为空气质量为A级的概率,求X的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列集合中,只有一个子集的是( )
A.{x∈R|x2-4=0} B.{x|x>9,或x<3}
C.{(x,y)|x2+y2=0} D.{x|x>9,且x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
阅读下面的算法:
第一步,输入两个实数a,b.
第二步:若a<b,则交换a,b的值,否则执行第三步.
第三步,输出a.
这个算法输出的是( )
A.a,b中的较大数 B.a,b中的较小数
C.原来的a的值 D.原来的b的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com