练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     检测部门决定对某市学校教室的空气质量进行检测,空气质量分为A、B、C三级.每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格.设各教室的空气质量相互独立,且每次检测的结果也相互独立.根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为,,.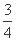

    (1) 在该市的教室中任取一间,估计该间教室空气质量合格的概率;

    (2) 如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为X,并以空气质量为A级的频率作为空气质量为A级的概率,求X的分布列及期望值.


     (1) 该间教室两次检测中,空气质量均为A级的概率为×=;

    该间教室两次检测中,空气质量一次为A级,另一次为B级的概率为2××=.

    设“该间教室的空气质量合格”为事件E,则

    P(E)=×+2××=.

    故估计该间教室的空气质量合格的概率为.

    (2) 方法一:由题意可知,X的取值为0,1,2,3,4.

    P(X=i)=(i=0,1,2,3,4).

    所以随机变量X的分布列为:

    X

    0

    1

    2

    3

    4

    P

      

      

      

      

      

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设m,n是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的是　　　　.(填序号) 

    ①若m∥α,n∥α,则m∥n;

    ②若m∥α,m∥β,则α∥β;

    ③若m∥n,m⊥α,则n⊥α;

    ④若m∥α,α⊥β,则m⊥β.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中,求过圆ρ=4cosθ的圆心,且垂直于极轴的直线的极坐标方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知椭圆C经过点A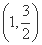,两个焦点分别为(-1,0),(1,0).

    (1) 求椭圆C的方程;

    (2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a0,a1,a2,…,a5为实数,则a3=　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知圆C的圆心为抛物线y2=-4x的焦点,又直线4x-3y-6=0与圆C相切,则圆C的标准方程为　　　　　　.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


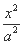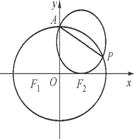
    已知椭圆C:+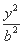=1(a>b>0)的上顶点为A,左、右焦点分别为F1,F2,且椭圆C过点P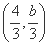,以AP为直径的圆恰好过右焦点F2.

    (1) 求椭圆C的方程;

    (2) 若动直线l与椭圆C有且只有一个公共点,试问:在x轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合U＝{1,2,3,4}，且M＝{x∈U|x2－5x＋p＝0}，若∁UM＝{1,4}，求实数p的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列关于程序框的功能描述正确的是(　　)

    A．(1)是处理框；(2)是判断框；(3)是终端框；(4)是输入、输出框

    B．(1)是终端框；(2)是输入、输出框；(3)是处理框；(4)是判断框

    C．(1)和(3)都是处理框；(2)是判断框；(4)是输入、输出框

    D．(1)和(3)的功能相同；(2)和(4)的功能相同

    查看答案和解析>>

    同步练习册答案