
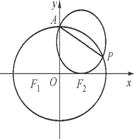
已知椭圆C: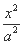 +
+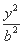 =1(a>b>0)的上顶点为A,左、右焦点分别为F1,F2,且椭圆C过点P
=1(a>b>0)的上顶点为A,左、右焦点分别为F1,F2,且椭圆C过点P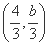 ,以AP为直径的圆恰好过右焦点F2.
,以AP为直径的圆恰好过右焦点F2.
(1) 求椭圆C的方程;
(2) 若动直线l与椭圆C有且只有一个公共点,试问:在x轴上是否存在两定点,使其到直线l的距离之积为1?若存在,请求出两定点坐标;若不存在,请说明理由.
(1) 因为椭圆过点P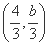 ,所以
,所以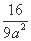 +
+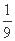 =1,解得a2=2.由题知A(0,b),F2(c,0),
=1,解得a2=2.由题知A(0,b),F2(c,0),
又以AP为直径的圆恰好过右焦点F2,所以AF2⊥F2P,所以 ·
·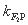 =-1,即-
=-1,即- ·
·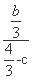 =-1,b2=c(4-3c).
=-1,b2=c(4-3c).
而b2=a2-c2=2-c2,所以c2-2c+1=0,解得c=1,
故椭圆C的方程是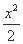 +y2=1.
+y2=1.
(2) ①当直线l斜率存在时,设直线l的方程为y=kx+p,代入椭圆方程得
(1+2k2)x2+4kpx+2p2-2=0.
因为直线l与椭圆C有且只有一个公共点,所以
Δ=16k2p2-4(1+2k2)(2p2-2)=8(1+2k2-p2)=0,
即1+2k2=p2.
设在x轴上存在两点 (s,0),(t,0),使其到直线l的距离之积为1,则
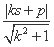 ·
·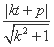 =
=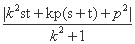 =1,
=1,
即(st+1)k2+kp(s+t)=0(*)或(st+3)k2+(s+t)kp+2=0 (**).
由(*)恒成立,得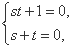
解得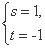 或
或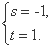
而(**)不恒成立.
②当直线l斜率不存在时,直线方程为x=±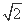 时,
时,
定点(-1,0),(1,0)到直线l的距离之积d1·d2=(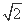 -1)(
-1)(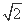 +1)=1.
+1)=1.
综上,存在两个定点(1,0),(-1,0),使其到直线l的距离之积为定值1.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
检测部门决定对某市学校教室的空气质量进行检测,空气质量分为A、B、C三级.每间教室的检测方式如下:分别在同一天的上、下午各进行一次检测,若两次检测中有C级或两次都是B级,则该教室的空气质量不合格.设各教室的空气质量相互独立,且每次检测的结果也相互独立.根据多次抽检结果,一间教室一次检测空气质量为A、B、C三级的频率依次为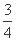 ,
, ,
, .
.
(1) 在该市的教室中任取一间,估计该间教室空气质量合格的概率;
(2) 如果对该市某中学的4间教室进行检测,记在上午检测空气质量为A级的教室间数为X,并以空气质量为A级的频率作为空气质量为A级的概率,求X的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列集合中,只有一个子集的是( )
A.{x∈R|x2-4=0} B.{x|x>9,或x<3}
C.{(x,y)|x2+y2=0} D.{x|x>9,且x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
若f(x)是偶函数且在(0,+∞)上减函数,又f(-3)=1,则不等式f(x)<1的解集为( )
A.{x|x>3或-3<x<0} B.{x|x<-3或0<x<3}
C.{x|x<-3或x>3} D.{x|-3<x<0或0<x<3}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com