
【题目】已知两条直线l1:y=m和l2:y= ![]() (m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2与函数y=|log2x|的图象从左至右相交于点C,D.记线段AC和BD在X轴上的投影长度分别为a,b,当m变化时,
(m>0),l1与函数y=|log2x|的图象从左至右相交于点A,B,l2与函数y=|log2x|的图象从左至右相交于点C,D.记线段AC和BD在X轴上的投影长度分别为a,b,当m变化时, ![]() 的最小值为( )
的最小值为( )
A.16 ![]()
B.8 ![]()
C.8 ![]()
D.4 ![]()
【答案】B
【解析】解:设A,B,C,D各点的横坐标分别为xA , xB , xC , xD ,
则﹣log2xA=m,log2xB=m;﹣log2xC= ![]() ,log2xD=
,log2xD= ![]() ;
;
∴xA=2﹣m , xB=2m , xC= ![]() ,xD=
,xD= ![]() .
.
∴a=|xA﹣xC|,b=|xB﹣xD|,
∴ ![]() =
= ![]() =|
=| 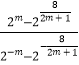 |=2m
|=2m ![]() =
= ![]() .
.
又m>0,∴m+ ![]() =
= ![]() (2m+1)+
(2m+1)+ ![]() ﹣
﹣ ![]() ≥2
≥2 ![]() ﹣
﹣ ![]() =
= ![]() (当且仅当m=
(当且仅当m= ![]() 时取“=”)
时取“=”)
∴ ![]() ≥
≥ ![]() =8
=8 ![]() .
.
故选B.
【考点精析】根据题目的已知条件,利用基本不等式在最值问题中的应用的相关知识可以得到问题的答案,需要掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”.


科目:高中数学 来源: 题型:
【题目】设f(x)=ln(x+1)+ ![]() +ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y=
+ax+b(a,b∈R,a,b为常数),曲线y=f(x)与直线y= ![]() x在(0,0)点相切.
x在(0,0)点相切.
(1)求a,b的值;
(2)证明:当0<x<2时,f(x)< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上![]() 件产品作为样本称出它们的重量(单位:克),重量的分组区间为
件产品作为样本称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() , ,
, ,![]() ,由此得到样本的频率分布直方图,如图所示.
,由此得到样本的频率分布直方图,如图所示.
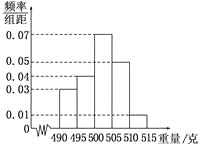
(1)根据频率分布直方图,求重量超过![]() 克的产品数量;
克的产品数量;
(2)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为重量超过
为重量超过![]() 克的产品数量,求
克的产品数量,求![]() 的分布列;
的分布列;
(3)从该流水线上任取![]() 件产品,求恰有
件产品,求恰有![]() 件产品的重量超过
件产品的重量超过![]() 克的概率.
克的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设ξ为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,ξ=0;当两条棱平行时,ξ的值为两条棱之间的距离;当两条棱异面时,ξ=1.
(1)求概率P(ξ=0);
(2)求ξ的分布列,并求其数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代著名的数学著作有10部算书,被称为“算经十书”.某校数学兴趣小组甲、乙、丙、丁四名同学对古代著名的数学著作产生浓厚的兴趣.一天,他们根据最近对这十部书的阅读本数情况说了这些话,甲:“乙比丁少”;乙:“甲比丙多”;丙:“我比丁多”; 丁:“丙比乙多”,他们说的这些话中,只有一个人说的是真实的,而这个人正是他们四个人中读书本数最少的一个(他们四个人对这十部书阅读本数各不相同).甲、乙、丙、丁按各人读书本数由少到多的排列是( )
A. 乙甲丙丁 B. 甲丁乙丙 C. 丙甲丁乙 D. 甲丙乙丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次性购物量 | 1至4件 | 5 至8件 | 9至12件 | 13至16件 | 17件及以上 |
顾客数(人) | x | 30 | 25 | y | 10 |
结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中的一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率.(注:将频率视为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 有以下性质:
有以下性质:
①过圆![]() 上一点
上一点![]() 的圆的切线方程是
的圆的切线方程是![]() .
.
②若不在坐标轴上的点![]() 为圆
为圆![]() 外一点,过
外一点,过![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,则
,则![]() 垂直
垂直![]() ,即
,即![]() .
.
(1)类比上述有关结论,猜想过椭圆![]() 上一点
上一点![]() 的切线方程 (不要求证明);
的切线方程 (不要求证明);
(2)若过椭圆![]() 外一点
外一点![]() (
(![]() 不在坐标轴上)作两直线,与椭圆相切于
不在坐标轴上)作两直线,与椭圆相切于![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是中华人民共和国成立70周年,某校党支部举办了一场“我和我的祖国”知识竞赛,满分100分,回收40份答卷,成绩均落在区间![]() 内,将成绩绘制成如下的频率分布直方图.
内,将成绩绘制成如下的频率分布直方图.
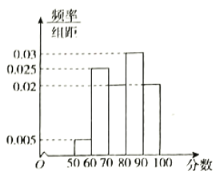
(1)估计知识竞赛成绩的中位数和平均数;
(2)从![]() ,
,![]() 分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于
分数段中,按分层抽样随机抽取5份答卷,再从对应的党员中选出3位党员参加县级交流会,求选出的3位党员中有2位成绩来自于![]() 分数段的概率.
分数段的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com