
设双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与 该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )
A.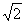 B.
B.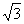 C.
C.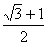 D.
D.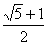
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
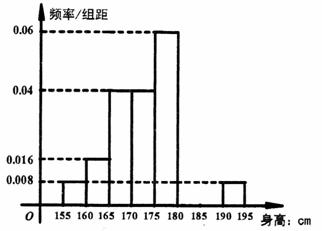
某学校进行体检,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50人身材均介于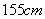 到
到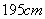 之间),现将抽取结果按如下方式分成八组:第一组
之间),现将抽取结果按如下方式分成八组:第一组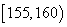 ,第二组
,第二组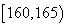 ,
, ,第八组
,第八组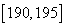 ,并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第六组的人数为4人。
,并按此分组绘制如下图所示的频率分布直方图,其中,第六组和第七组还没有绘制完成,已知第一组与第八组人数相同,第六组的人数为4人。
(1)求第七组的频率;
(2)若从身高属于第一组和第六组的所有男生中随机抽取两名男生,求两人身高差距不超过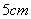 的概率
的概率 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
在空间直角坐标系中,点P(1,3,-5)关于平面xoy对称的点的坐标是 ( )
A.(-1,3,-5) B.(1,3,5) C..(1,-3,5) D.(-1,-3,5)
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,四棱锥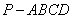 的底面
的底面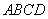 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中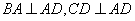 ,
, ,平面
,平面 底面
底面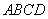 ,
, 是
是 的中点.
的中点.
(1)求证: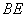 //平面
//平面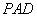 ;
;
(2)求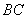 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;
(3)线段PC上是否存在一点M,使得AM⊥平面PBD,如果存在,求出PM的长度;如果不存在,请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com