
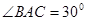 ,
,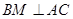 交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,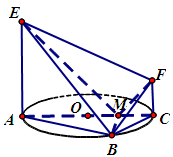
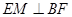 ;
;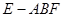 的体积
的体积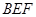 和平面
和平面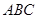 所成的锐二面角的正切值.
所成的锐二面角的正切值.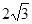 ;(理科)1
;(理科)1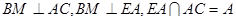 ,∴
,∴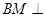 面
面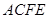 ,从而
,从而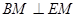 ,在梯形
,在梯形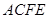 中,证明
中,证明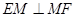 ,从而
,从而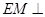 面
面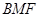 ,∴
,∴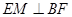 ;(2)(文科)求三棱锥的体积,关键是确定三棱锥的高,往往需要等体积转化,
;(2)(文科)求三棱锥的体积,关键是确定三棱锥的高,往往需要等体积转化,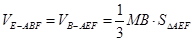 ,可得;(2)理科,题中未给出两个半平面的交线,首先确定交线,延长
,可得;(2)理科,题中未给出两个半平面的交线,首先确定交线,延长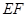 交
交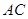 于
于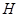 ,连结
,连结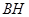 ,然后先找二面角的平面角,再计算,过
,然后先找二面角的平面角,再计算,过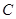 做
做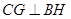 ,垂足
,垂足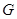 ,连接
,连接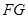 ,证明
,证明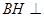 面
面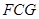 ,则
,则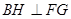 ,
,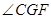 就是所求二面角的平面角,计算即得结果.
就是所求二面角的平面角,计算即得结果.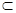 面ABC,∴EA⊥MB,∴MB⊥AC,AC∩EA=A,∴MB⊥面ACEF,
面ABC,∴EA⊥MB,∴MB⊥AC,AC∩EA=A,∴MB⊥面ACEF,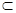 面ACEF,∴EM⊥MB,在直角梯形ACEF中,EA=3,FC=1,AC=4,∴EF=
面ACEF,∴EM⊥MB,在直角梯形ACEF中,EA=3,FC=1,AC=4,∴EF=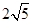 ,在Rt△ABC中, ∵
,在Rt△ABC中, ∵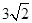 ,MF=
,MF=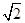 ,∵EF2=EM2+MF2,∴EM⊥MF,
,∵EF2=EM2+MF2,∴EM⊥MF, 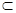 面MBF,∴EM⊥BF 8分
面MBF,∴EM⊥BF 8分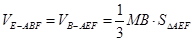 ,在直角梯形ACEF中,
,在直角梯形ACEF中,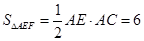 ,
,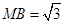 ,∴
,∴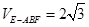 14分
14分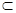 面ABC,∴BH⊥FC,∵FC∩CG=C,∴BH⊥面FCG,∵FG
面ABC,∴BH⊥FC,∵FC∩CG=C,∴BH⊥面FCG,∵FG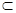 面FCG,∴BH⊥FG,∴∠CGF为平面BEF与平面ABC所成的二面角的平面角,在直角梯形ACEF中,CH=2,,在△BCH中,CH=2,BC=2,∠BCH=
面FCG,∴BH⊥FG,∴∠CGF为平面BEF与平面ABC所成的二面角的平面角,在直角梯形ACEF中,CH=2,,在△BCH中,CH=2,BC=2,∠BCH=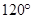 ,∴CG=1,在Rt△CGF中,FC=1,
,∴CG=1,在Rt△CGF中,FC=1,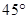 ,平面BEF与平面ABC所成的锐二面角正切值为1 14分
,平面BEF与平面ABC所成的锐二面角正切值为1 14分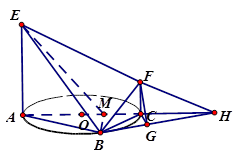


科目:高中数学 来源:不详 题型:解答题
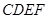 中,
中,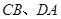 是梯形的高,
是梯形的高,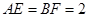 ,
,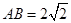 ,现将梯形沿
,现将梯形沿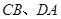 折起,使
折起,使 ,且
,且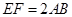 ,得一简单组合体
,得一简单组合体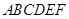 如图所示,已知
如图所示,已知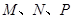 分别为
分别为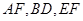 的中点.
的中点.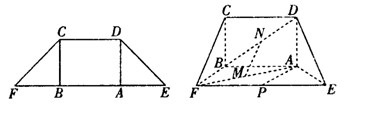
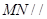 平面
平面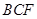 ;
; 平面
平面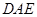 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com