
(1)已知a>b>c,且a+b+c=0,用分析法求证:<a.
(2)f(x)=,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳猜想一般性结论,并给出证明.
(1)详见解析;(2)都为,猜想f(x)+f(1-x)=.
【解析】
试题分析:(1)注意题目指定用分析法证,要特别注意分析法的书写格式:要证<a,只需证…,直到归结到一个由已知很容易得到其成立的不等式为止;其分析的方向是将无理不等式不断转化为有理不等式,在转化的过程中要注意已知条件的使用,同时不必找充要条件,只须找充分条件即可;(2)先由已知函数计算出f(0)+f(1),f(-1)+f(2),f(-2)+f(3)的值,寻找规律不难猜想出:其自变量和为1的两个自变量所对应的函数值之和也为定值:;证明也就只须用函数的解析式计算出f(x)+f(1-x)的值即可.
试题解析:(1)证明:要证<a,只需证b2-ac<3a2.
∵ a+b+c=0,∴ 只需证b2+a(a+b)<3a2,只需证2a2-ab-b2>0,
只需证(a-b)(2a+b)>0,只需证(a-b)(a-c)>0.
∵ a>b>c,∴ a-b>0,a-c>0,∴ (a-b)(a-c)>0显然成立.故原不等式成立;
(2)f(0)+f(1)=+=+=+=,
同理可得:f(-1)+f(2)=,f(-2)+f(3)=.
由此猜想f(x)+f(1-x)=.
证明:f(x)+f(1-x)=+
=+=+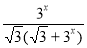 =
=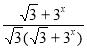 =.
=.
考点:1.不等式的证明方法:分析法;2.归纳、猜想与证明.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:解答题
已知 是
是 的导函数,
的导函数,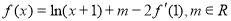 ,且函数
,且函数 的图象过点
的图象过点 .
.
(1)求函数 的表达式;
的表达式;
(2)求函数 的单调区间和极值.
的单调区间和极值.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
若x、y满足约束条件 ,则z=x+2y的取值范围( )
,则z=x+2y的取值范围( )
A.[2,6] B.[2,5] C.[3,6] D.(3,5]
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:解答题
已知函数 的减区间是(-2,2)
的减区间是(-2,2)
(1)试求m,n的值;
(2)求过点 且与曲线
且与曲线 相切的切线方程;
相切的切线方程;
(3)过点A(1,t),是否存在与曲线 相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
相切的3条切线,若存在,求实数t的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:选择题
斜率为 的直线
的直线 过双曲线
过双曲线 的右焦点,且与双曲线的左右两支都相交,则双曲线的离心率
的右焦点,且与双曲线的左右两支都相交,则双曲线的离心率 的取值范围是 ( )
的取值范围是 ( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
设离散型随机变量X的概率分布列如下表:
X | 1 | 2 | 3 | 4 |
P |
| p |
|
|
则p等于( )
A. B.
B.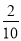 C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com