
分析 (Ⅰ)写出约束条件,画出图象即可,
(Ⅱ)设出目标函数,欲求利润最大,即求可行域中的最优解,将目标函数看成是一条直线,分析目标函数Z与直线截距的关系,进而求出最优解.
解答 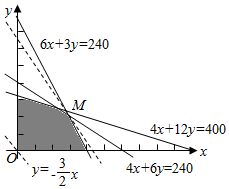 解:(Ⅰ)由已知x,y满足的数学关系式为$\left\{\begin{array}{l}{6x+3y≤240}\\{4x+12y≤400}\\{4x+6y≤240}\\{x≥0}\\{y≥0}\end{array}\right.$,
解:(Ⅰ)由已知x,y满足的数学关系式为$\left\{\begin{array}{l}{6x+3y≤240}\\{4x+12y≤400}\\{4x+6y≤240}\\{x≥0}\\{y≥0}\end{array}\right.$,
该二元一次不等式组所表示的平面区域为图中的阴影部分.
(Ⅱ)解:设利润为z万元,则目标函数z=900x+600y,所以y=-$\frac{3}{2}$x+$\frac{z}{600}$,这是斜率为-$\frac{3}{2}$,在y轴上的截距为$\frac{z}{600}$的一族平行直线.
当$\frac{z}{600}$取最大值时,z的值最大,又因为x,y满足约束条件,所以由图可知,当直线z=900x+600y经过可行域中的点M时,截距$\frac{z}{600}$的值最大,即z的值最大.
解方程组$\left\{\begin{array}{l}{6x+3y=240}\\{4x+6y=240}\end{array}\right.$,得点M的坐标为(30,20),
所以Zmax=900×30+600×20=39000.
故每天生产甲种产品30吨,乙种产品20吨时利润最大,且最大利润为39000元.
点评 本题主要考查生活中的优化问题,利用条件建立二元二次不等式组,利用线性规划的知识进行求解是解决本题的关键.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120),历年中日泄流量在区间[30,60)的年平均天数为156,一年按364天计.
某地政府拟在该地一水库上建造一座水电站,用泄流水量发电.图是根据该水库历年的日泄流量的水文资料画成的日泄流量X(单位:万立方米)的频率分布直方图(不完整),已知X∈[0,120),历年中日泄流量在区间[30,60)的年平均天数为156,一年按364天计.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-∞,-\frac{1}{2}}]∪[{1,+∞})$ | B. | $({-∞,-1}]∪[{\frac{1}{2},+∞})$ | C. | $({-∞,0}]∪[{\frac{1}{2},+∞})$ | D. | $({-∞,-\frac{1}{2}}]∪[{0,+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
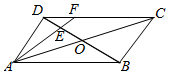 在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com