
分析 设公差为d,运用等差数列的求和公式,结合条件可得a1=-8d,由通项公式可判断(1);由d<0,结合数列的各项的符号,即可判断(2);由等差数列的求和公式,解方程结合m,k为正整数即可判断(3),(4).
解答 解:由数列{an}是单调递减的等差数列,设公差为d,S6=S11,
可得6a1+$\frac{6×5}{2}$d=11a1+$\frac{11×10}{2}$d,
化简可得a1=-8d,
(1)a9=a1+8d=0,故正确;
(2)由an=a1+(n-1)d=(n-9)d,
由d<0,a1>0,…,a8=-d>0,a9=0,a10<0,
可得当n=8或n=9时,Sn取最大值,故正确;
(3)Sn=na1+$\frac{n(n-1)}{2}$d=d•$\frac{{n}^{2}-17n}{2}$,
由Sn=0,可得n2-17n=0,解得n=17∈N,
故存在正整数17使得S17=0;
(4)由Sm=d•$\frac{{m}^{2}-17m}{2}$,S2m=d•$\frac{4{m}^{2}-34m}{2}$,
由Sm=S2m,可得m2-17m=4m2-34m,
解得m=0或m=$\frac{17}{3}$.
则不存在存在正整数m使得Sm=S2m.
其中正确的是:(1),(2),(3).
故答案为:(1),(2),(3).
点评 本题考查等差数列的通项公式和求和公式的运用,考查数列的最值的求法,考查方程思想,以及化简整理的运算能力和判断能力,属于中档题.


科目:高中数学 来源: 题型:解答题
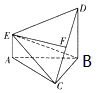 如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点.
如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (-$\frac{1}{2}$,0)∪(0,$\frac{1}{2}$) | C. | (0,2) | D. | (-2,0)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$] | B. | [$\frac{1}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$] | D. | [$\frac{\sqrt{2}}{2}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com