
���� ������|F1F2|=2����$��\sqrt{2}��\frac{{\sqrt{6}}}{2}��$�ڸ���Բ�ϣ����a=2��$b=\sqrt{3}$���ɴ��ܳ���ԲC�ķ��̣�
������P��x1��y1����Q��x2��y2�����Ƶ���$|P{F_2}|=\frac{1}{2}��4-{x_1}��=2-\frac{1}{2}{x_1}$������OM��OP�������������Ƶ���$|PM|=\frac{1}{2}{x_1}$���ɴ������|F2P|+|F2Q|+|PQ|Ϊ��ֵ��
��� �⣺����F1��F2�ֱ�����ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��a��b��0��$���������㣬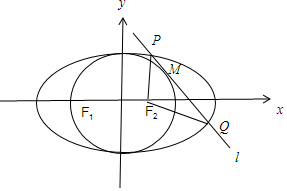
��|F1F2|=2����$��\sqrt{2}��\frac{{\sqrt{6}}}{2}��$�ڸ���Բ�ϣ�
�����⣬��c=1����a2-b2=1����
�ֵ�$��\sqrt{2}��\frac{{\sqrt{6}}}{2}��$�ڸ���Բ�ϣ���$\frac{2}{a^2}+\frac{3}{{2{b^2}}}=1$����
�ɢ٢��������a=2��$b=\sqrt{3}$��
����ԲC�ķ���Ϊ$\frac{x^2}{4}+\frac{y^2}{3}=1$��
������P��x1��y1����Q��x2��y2����
$\frac{{{x_1}^2}}{4}+\frac{{{y_1}^2}}{3}=1��|{x_1}|��2��$��$|P{F_2}{|^2}={��{x_1}-1��^2}+{y_1}^2={��{x_1}-1��^2}+3��1-\frac{{{x_1}^2}}{4}��=\frac{1}{4}{��{x_1}-4��^2}$��
��$|P{F_2}|=\frac{1}{2}��4-{x_1}��=2-\frac{1}{2}{x_1}$��
����OM��OP������������֪��
$|PM{|^2}=|OP{|^2}-|OM{|^2}={x_1}^2+{y_1}^2-3={x_1}^2+3��1-\frac{{{x_1}^2}}{4}��-3=\frac{1}{4}{x_1}^2$��
��$|PM|=\frac{1}{2}{x_1}$��
��$|P{F_2}|+|PM|=2-\frac{1}{2}{x_1}+\frac{1}{2}{x_1}=2$��
ͬ�������$|Q{F_2}|+|QM|=2-\frac{1}{2}{x_2}+\frac{1}{2}{x_2}=2$��
��|F2P|+|F2Q|+|PQ|=2+2=4Ϊ��ֵ��
���� ���⿼����Բ���̵��������߶κ��Ƿ�Ϊ��ֵ���ж���������������֤��������������������ռ���������������ȼ�ת��˼�롢���ν��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-�ޣ�-\frac{1}{2}}]��[{1��+��}��$ | B�� | $��{-�ޣ�-1}]��[{\frac{1}{2}��+��}��$ | C�� | $��{-�ޣ�0}]��[{\frac{1}{2}��+��}��$ | D�� | $��{-�ޣ�-\frac{1}{2}}]��[{0��+��}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����߶�˳����β���ӣ����õ�ͼ��һ����ƽ��ͼ�� | |
| B�� | һ��ֱ�ߺ�����ƽ��ֱ�߶��ཻ��������ֱ�߹��� | |
| C�� | ����ƽ�е�����ֱ��һ��ȷ������ƽ�� | |
| D�� | ����������ֱ�߶��ཻ��ֱ��һ��������ֱ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com