
【题目】已知函数f(x)=xlnx+ax(a∈R).
(Ⅰ)当a=0,求f(x)的最小值;
(Ⅱ)若函数g(x)=f(x)+lnx在区间[1,+∞)上为增函数,求实数a的取值范围;
(Ⅲ)过点P(1,﹣3)恰好能作函数y=f(x)图象的两条切线,并且两切线的倾斜角互补,求实数a的取值范围.
【答案】解:(I)f(x)的定义域为(0,+∞) ![]() ,
,
当x∈(0,+∞)时,f'(x),f(x)的变化的情况如下:
x |
|
|
|
f'(x) | ﹣ | 0 | + |
f(x) | 极小值 |
∴f(x)的最小值是f( ![]() )=﹣
)=﹣ ![]() .
.
(Ⅱ)由题意得: ![]()
∵函数g(x)在区间[1,+∞)上为增函数,
∴当x∈[1,+∞)时g'(x)≥0,即 ![]() 在[1,+∞)上恒成立,
在[1,+∞)上恒成立,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() 在[1,+∞)上递增,
在[1,+∞)上递增,
∴﹣(a+1)≤h(1)=1,
∴a≥﹣2
(Ⅲ)设两切点A(x1 , f(x1)),B(x2 , f(x2)),f'(x)=lnx+1+a
则函数y=f(x)在A,B处的切线方程分别为y=(lnx1+1+a)(x﹣x1)+x1lnx1+ax1=(lnx1+1+a)x﹣x1 ,
∴y=(lnx2+1+a)(x﹣x2)+x2lnx2+ax2=(lnx2+1+a)x﹣x2
且lnx1+1+a+lnx2+1+a=0
即 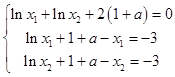 也即
也即 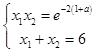
即x1 , x2是方程t2﹣6t+e﹣2(a+1)=0的两个正根,
∴△=36﹣4e﹣2(a+1)>0,
∴a>﹣1﹣ln3
【解析】(Ⅰ)求导函数,确定函数的单调性,即可求f(x)的最小值;(Ⅱ)函数g(x)在区间[1,+∞)上为增函数,可得当x∈[1,+∞)时g'(x)≥0,即 ![]() 在[1,+∞)上恒成立,求出左边的最小值,即可求实数a的取值范围;(Ⅲ)求出函数y=f(x)在A,B处的切线方程,利用过点P(1,﹣3),两切线的倾斜角互补,建立方程组,即可求实数a的取值范围.
在[1,+∞)上恒成立,求出左边的最小值,即可求实数a的取值范围;(Ⅲ)求出函数y=f(x)在A,B处的切线方程,利用过点P(1,﹣3),两切线的倾斜角互补,建立方程组,即可求实数a的取值范围.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】曲线 ![]() 是平面内到定点
是平面内到定点 ![]() 的距离与到定直线
的距离与到定直线 ![]() 的距离之和为
的距离之和为 ![]() 的动点
的动点 ![]() 的轨迹.则曲线
的轨迹.则曲线 ![]() 与
与 ![]() 轴交点的坐标是________________;又已知点
轴交点的坐标是________________;又已知点 ![]() (
(![]() 为常数),那么
为常数),那么 ![]() 的最小值
的最小值 ![]() ________________.
________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式: 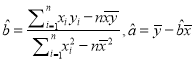 .
.
参考数据: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,A,B,C是双曲线 ![]() =1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是( )
=1(a>0,b>0)上的三个点,AB经过原点O,AC经过右焦点F,若BF⊥AC且|BF|=|CF|,则该双曲线的离心率是( ) 
A.![]()
B.![]()
C.![]()
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 若a1=1,且Sn=tan﹣ ![]() ,其中n∈N*.
,其中n∈N*.
(1)求实数t的值和数列{an}的通项公式;
(2)若数列{bn}满足bn=log3a2n , 求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数对(x,y),设映射f:(x,y)→( ![]() ,
, ![]() ),并定义|(x,y)|=
),并定义|(x,y)|= ![]() ,若|f[f(f(x,y))]|=4,则|(x,y)|的值为( )
,若|f[f(f(x,y))]|=4,则|(x,y)|的值为( )
A.4 ![]()
B.8 ![]()
C.16 ![]()
D.32 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωx+cosωx+c(ω>0,x∈R,c是常数)图象上的一个最高点为(
sinωx+cosωx+c(ω>0,x∈R,c是常数)图象上的一个最高点为( ![]() ,1),与其相邻的最低点是(
,1),与其相邻的最低点是( ![]() ,﹣3).
,﹣3).
(1)求函数f(x)的解析式及其对称中心;
(2)在△ABC中,角A,B,C所对的边分别为a,b,c,且 ![]() =﹣
=﹣ ![]() ac,试求函数f(A)的取值范围.
ac,试求函数f(A)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元。
(1)设铁栅长为![]() 米,一堵砖墙长为
米,一堵砖墙长为![]() 米,求函数
米,求函数![]() 的解析式;
的解析式;
(2)为使仓库总面积![]() 达到最大,正面铁栅应设计为多长?
达到最大,正面铁栅应设计为多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com