练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．如图，小明从街道的E处出发，先到F处与小红会合，再一起到位于G处的老年公寓参加志愿者活动，则小明到老年公寓可以选择的最短路径条数为（　　）
    A．24B．18C．12D．9

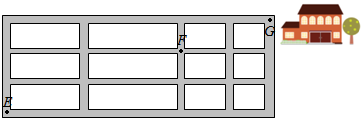
    分析 从E到F最短的走法，无论怎样走，一定包括4段，其中2段方向相同，另2段方向相同，每种最短走法，即是从4段中选出2段走东向的，选出2段走北向的，由组合数可得最短的走法，同理从F到G，最短的走法，有C31=3种走法，利用乘法原理可得结论．

    解答 解：从E到F，每条东西向的街道被分成2段，每条南北向的街道被分成2段，
    从E到F最短的走法，无论怎样走，一定包括4段，其中2段方向相同，另2段方向相同，
    每种最短走法，即是从4段中选出2段走东向的，选出2段走北向的，故共有C42C22=6种走法．
    同理从F到G，最短的走法，有C31C22=3种走法．
    ∴小明到老年公寓可以选择的最短路径条数为6×3=18种走法．
    故选：B．

    点评 本题考查排列组合的简单应用，得出组成矩形的条件和最短走法是解决问题的关键，属基础题

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．如图流程图表示的算法是（　　）
    A．输出c，b，aB．输出最大值C．输出最小值D．比较a，b，c大小

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在△ABC中，已知AB=16，AC=12，BC=10，点I为△ABC内一点，且存在实数λ、μ，使得$\overrightarrow{AI}$=$\overrightarrow{AB}$+λ（$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$），$\overrightarrow{AI}$=$\overrightarrow{AC}$+μ（$\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}$+$\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$），则$\frac{\overrightarrow{CI}•\overrightarrow{CB}}{|\overrightarrow{BC}|}$的值为（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知等差数列{an}前9项的和为27，a10=8，则a100=（　　）
    A．100B．99C．98D．97

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．设向量$\overrightarrow{a}$=（m，1），$\overrightarrow{b}$=（1，2），且|$\overrightarrow{a}$+$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2，则m=-2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（　　）
    A．y=xB．y=lgxC．y=2xD．y=$\frac{1}{\sqrt{x}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知{an}为等差数列，Sn为其前n项和．若a1=6，a3+a5=0，则S6=6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．某单位工作人员的构成如图所示，现采用分层抽样的方法抽取工作人员进行薪资情况调查，若管理人员抽取了6人，则抽到的教师人数为9．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|≤$\frac{π}{2}$），x=-$\frac{π}{4}$为f（x）的零点，x=$\frac{π}{4}$为y=f（x）图象的对称轴，且f（x）在（$\frac{π}{18}$，$\frac{5π}{36}$）上单调，则ω的最大值为（　　）
    A．11B．9C．7D．5

    查看答案和解析>>

    同步练习册答案