Question

10．在△ABC中，已知AB=16，AC=12，BC=10，点I为△ABC内一点，且存在实数λ、μ，使得$\overrightarrow{AI}$=$\overrightarrow{AB}$+λ（$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$），$\overrightarrow{AI}$=$\overrightarrow{AC}$+μ（$\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}$+$\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$），则$\frac{\overrightarrow{CI}•\overrightarrow{CB}}{|\overrightarrow{BC}|}$的值为（　　）

• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 运用向量的加法运算可得即有$\overrightarrow{BI}$=λ（$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$），结合平行四边形法则，可得BI平分内角ABC，同理可得CI平分内角ACB，由内角平分线定理可得AI平分内角BAC．即I为△ABC的内心，设内切圆的半径为r，运用余弦定理和面积公式，即可得到r，过I作ID⊥BC，垂足为D，运用二倍角的余弦公式，以及同角的商数关系，计算可得CD=3，再由向量的数量积定义可得$\frac{\overrightarrow{CI}•\overrightarrow{CB}}{|\overrightarrow{BC}|}$=CD=3．

解答 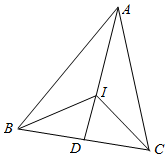解：$\overrightarrow{AI}$=$\overrightarrow{AB}$+$\overrightarrow{BI}$=$\overrightarrow{AB}$+λ（$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$），
即有$\overrightarrow{BI}$=λ（$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$+$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$），
由$\frac{\overrightarrow{BA}}{|\overrightarrow{BA}|}$，$\frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}$分别为$\overrightarrow{BA}$，$\overrightarrow{BC}$的单位向量，
结合平行四边形法则，可得BI平分内角ABC，
同理由$\overrightarrow{AI}$=$\overrightarrow{AC}$+μ（$\frac{\overrightarrow{CA}}{|\overrightarrow{CA}|}$+$\frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}$），可得CI平分内角ACB，
由内角平分线定理可得AI平分内角BAC．
即I为△ABC的内心，设内切圆的半径为r，
由余弦定理可得cos∠ACB=$\frac{A{C}^{2}+B{C}^{2}-A{C}^{2}}{2AC•BC}$=$\frac{144+100-256}{2×12×10}$=-$\frac{1}{20}$，
sin∠ACB=$\sqrt{1-（-\frac{1}{20}）^{2}}$=$\frac{\sqrt{399}}{20}$，
即有△ABC的面积为S=$\frac{1}{2}$AC•BC•sin∠ACB=$\frac{1}{2}$×12×10×$\frac{\sqrt{399}}{20}$=3$\sqrt{399}$，
又S=$\frac{1}{2}$r（AC+CB+AB）=$\frac{1}{2}$r（12+10+16）=19r，
解得r=$\frac{3\sqrt{399}}{19}$，
过I作ID⊥BC，垂足为D，
由sin$\frac{∠ACB}{2}$=$\sqrt{\frac{1-cos∠ACB}{2}}$=$\sqrt{\frac{21}{40}}$，cos$\frac{∠ACB}{2}$=$\sqrt{\frac{1+cos∠ACB}{2}}$=$\sqrt{\frac{19}{40}}$，
在△CID中，CD=DI•cot$\frac{∠ACB}{2}$=$\frac{3\sqrt{399}}{19}$×$\sqrt{\frac{19}{21}}$=3．
则$\frac{\overrightarrow{CI}•\overrightarrow{CB}}{|\overrightarrow{BC}|}$=$\frac{|\overrightarrow{CI}|•|\overrightarrow{CB}|•cos\frac{∠ACB}{2}}{|\overrightarrow{CB}|}$=|$\overrightarrow{CI}$|•cos$\frac{∠ACB}{2}$=|$\overrightarrow{CD}$|=3．
故选：B．

点评 本题考查向量的数量积的定义和性质，同时考查向量共线定理的运用，三角形的余弦定理和面积公式的运用，考查三角函数的化简整理的运算能力，属于中档题．