练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设a，b，c为一个三角形的三边，s＝(a＋b＋c)，且s2＝2ab，试证：s<2a.


    证明　要证s<2a，由于s2＝2ab，所以只需证s<，即证b<s.

    因为s＝(a＋b＋c)，所以只需证2b<a＋b＋c，即证b<a＋c.

    由于a，b，c为一个三角形的三条边，所以上式成立．于是原命题成立．   


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图所示四个图形中，着色三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面中有命题：等腰三角形底边上任一点到两腰距离之和等于一腰上的高．把此结论类比到空间的正三棱锥，猜想并证明相关结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    学习合情推理后，甲、乙两位同学各举一个例子．

    甲：由“若三角形周长为l，面积为S，则其内切圆半径r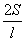＝”类比可得“若三棱锥表面积为S，体积为V，则其内切球半径r＝”；

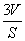    乙：由“若直角三角形两直角边长分别为a、b，则其外接圆半径r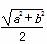＝”类比可得“若三棱锥三条侧棱两两垂直，侧棱长分别为a、b、c，则其外接球半径r＝．

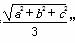    这两位同学类比得出的结论正确的是________．

    这两位同学类比得出的结论正确的是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示是按照一定规律画出的一列“树型”图，设第n个图有an个“树枝”，则an＋1与an(n∈N*)之间的关系是______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l，m，平面α，β，且l⊥α，m⊂β，给出下列四个命题：①若α∥β，则l⊥m；②若l⊥m，则α∥β；③若α⊥β，则l⊥m；④若l∥m，则α⊥β.

    其中正确命题的个数是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a≥b>0，求证：3a3＋2b3≥3a2b＋2ab2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     (1)当c<0时，若ac>bc，则a<b.请写出该命题的逆命题、否命题、逆否命题，并分别判断真假；

    (2)p：对角线互相垂直的四边形是菱形，q：对角线互相平分的四边形是菱形，请写出“p或q”，“p且q”，“非p”形式的命题．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等轴双曲线x2－y2＝a2截直线4x＋5y＝0所得弦长为，则双曲线的实轴长是________．

    查看答案和解析>>

    同步练习册答案