
在平面中有命题:等腰三角形底边上任一点到两腰距离之和等于一腰上的高.把此结论类比到空间的正三棱锥,猜想并证明相关结论.
科目:高中数学 来源: 题型:
已知x1>0,x1≠1且xn+1=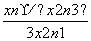 (n=1,2,…),试证:“数列{xn}对任意的正整数n都满足xn>xn+1”,当此题用反证法否定结论时应为____________________.
(n=1,2,…),试证:“数列{xn}对任意的正整数n都满足xn>xn+1”,当此题用反证法否定结论时应为____________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
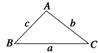
如图所示,在△ABC中,射影定理可表示为a=b·cos C+c·cos B,其中a,b,c分别为角A,B,C的对边,类比 上述定理,写出对空间四面体性质的猜想.
上述定理,写出对空间四面体性质的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知△ABC中,AD⊥BC于D,三边是a,b,c,则有a=ccos B+bcos C;类比上述推理结论,写出下列条件下的结论:四面体P—ABC中,△ABC,△PAB,△PBC,△PCA的面积分别是S,S1,S2,S3,二面角P—AB—C,P—BC—A,P—AC—B的度数分别是α,β,γ,则S=__________________________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com