练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

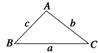
    如图所示，在△ABC中，射影定理可表示为a＝b·cos C＋c·cos B，其中a，b，c分别为角A，B，C的对边，类比上述定理，写出对空间四面体性质的猜想．


    解　如图所示，在四面体P－ABC中，设S1，S2，S3，S分别表示△PAB，△PBC，△PCA，△ABC的面积，α，β，γ依次表示面PAB，面PBC，面PCA与底面ABC所成二面角的大小．

    我们猜想射影定理类比推理到三维空间，其表现形式应为：S＝S1·cos α＋S2·cos β＋S3·cos γ.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    下列说法正确的是(　　)

    A．命题“若x2＝1，则x＝1”的否命题为“若x2＝1，则x≠1”

    B．命题“∃x0∈R，x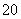＋x0－1＜0”的否定是“∀x∈R，x2＋x－1＞0”

    C．命题“若x＝y，则sin x＝sin y”的逆否命题为假命题

    D．若“p或q”为真命题，则p，q中至少有一个为真命题

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示四个图形中，着色三角形的个数依次构成一个数列的前4项，则这个数列的一个通项公式为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ax＋ (a>1)，用反证法证明方程f(x)＝0没有负数根．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    把下面在平面内成立的结论类比地推广到空间，结论仍然正确的是________．(填序号)

    ①如果一条直线与两条平行线中的一条相交，则也与另一条相交；

    ②如果一条直线与两条平行线中的一条垂直，则也与另一条垂直；

    ③如果两条直线同时与第三条直线相交，则这两条直线相交或平行；

    ④如果两条直线同时与第三条直线垂直，则这两条直线平行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    正方形ABCD中，对角线AC⊥BD.运用类比的方法，猜想正方体ABCD—A1B1C1D1中，相关结论：________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面中有命题：等腰三角形底边上任一点到两腰距离之和等于一腰上的高．把此结论类比到空间的正三棱锥，猜想并证明相关结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    学习合情推理后，甲、乙两位同学各举一个例子．

    甲：由“若三角形周长为l，面积为S，则其内切圆半径r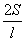＝”类比可得“若三棱锥表面积为S，体积为V，则其内切球半径r＝”；

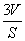    乙：由“若直角三角形两直角边长分别为a、b，则其外接圆半径r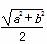＝”类比可得“若三棱锥三条侧棱两两垂直，侧棱长分别为a、b、c，则其外接球半径r＝．

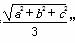    这两位同学类比得出的结论正确的是________．

    这两位同学类比得出的结论正确的是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     (1)当c<0时，若ac>bc，则a<b.请写出该命题的逆命题、否命题、逆否命题，并分别判断真假；

    (2)p：对角线互相垂直的四边形是菱形，q：对角线互相平分的四边形是菱形，请写出“p或q”，“p且q”，“非p”形式的命题．

    查看答案和解析>>

    同步练习册答案