练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     (1)当c<0时，若ac>bc，则a<b.请写出该命题的逆命题、否命题、逆否命题，并分别判断真假；

    (2)p：对角线互相垂直的四边形是菱形，q：对角线互相平分的四边形是菱形，请写出“p或q”，“p且q”，“非p”形式的命题．


    解　(1)逆命题：当c<0时，若a<b，则ac>bc(真命题)

    否命题：当c<0时，若ac≤bc，则a≥b(真命题)

    逆否命题：当c<0时，若a≥b，则ac≤bc(真命题)．

    (2)p或q：对角线互相垂直的四边形或对角线互相平分的四边形是菱形．

    p且q：对角线互相垂直的四边形且对角线互相平分的四边形是菱形．

    非p：对角线互相垂直的四边形不是菱形．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


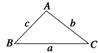
    如图所示，在△ABC中，射影定理可表示为a＝b·cos C＋c·cos B，其中a，b，c分别为角A，B，C的对边，类比上述定理，写出对空间四面体性质的猜想．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设a，b，c为一个三角形的三边，s＝(a＋b＋c)，且s2＝2ab，试证：s<2a.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    与命题“若x∈A，则y∉A”等价的命题是________．(填序号)

    ①若x∉A，则y∉A；②若y∉A，则x∈A；

    ③若x∉A，则y∈A；④若y∈A，则x∉A.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列四个命题中

    ①“k＝1”是“函数y＝cos2kx－sin2kx的最小正周期为π”的充要条件；

    ②“a＝3”是“直线ax＋2y＋3a＝0与直线3x＋(a－1)y＝a－7相互垂直”的充要条件；

    ③函数y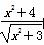＝的最小值为2.

    其中是假命题的为________(将你认为是假命题的序号都填上)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知下列三个方程：x2＋4ax－4a＋3＝0，x2＋(a－1)x＋a2＝0，x2＋2ax－2a＝0至少有一个方程有实数根，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    命题p：若a≥b则c>d，命题q：若e≤f则a<b，若p为真，q的否命题为真，则“c≤d”是“e≤f”的________条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    判断下列命题的真假．

    (1)对于任意x，若x－3＝0，则x－3≤0；

    (2)若x＝3或x＝5，则(x－3)(x－6)＝0.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    点A、B分别是椭圆＋＝1长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于x轴上方，PA⊥PF.求点P的坐标．

    查看答案和解析>>

    同步练习册答案