练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    正方形ABCD中，对角线AC⊥BD.运用类比的方法，猜想正方体ABCD—A1B1C1D1中，相关结论：________________________.


    对角面AA1C1C⊥BB1D1D


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    A、B、C、D、E五人站成一排，如果A必须站在B的左边(A、B可以不相邻)，则不同排法有                                                         (　　)

    A．24种         B．60种        C．90种          D．120种

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在一容器内装有浓度r%的溶液a升，注入浓度为p%的溶液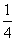a升，搅匀后再倒出溶液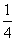a升，这叫一次操作，设第n次操作后容器内溶液的浓度为bn，计算b1、b2、b3，并归纳出计算公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    类比平面直角坐标系中△ABC的重心G(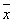，)的坐标公式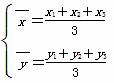 (其中A(x1，y1)、B(x2，y2)、C(x3，y3))，猜想以A(x1，y1，z1)、B(x2，y2，z2)、C(x3，y3，z3)、D(x4，y4，z4)为顶点的四面体A—BCD的重心G(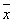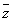，，)的公式为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


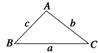
    如图所示，在△ABC中，射影定理可表示为a＝b·cos C＋c·cos B，其中a，b，c分别为角A，B，C的对边，类比上述定理，写出对空间四面体性质的猜想．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知命题：平面直角坐标系xOy中，△ABC的顶点A(－p,0)和C(p,0)，顶点B在椭圆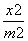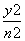＋＝1 (m>n>0，p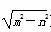＝)上，椭圆的离心率是e，则＝.

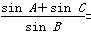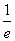    将该命题类比到双曲线中，给出一个命题：__________________________________

    ________________________________________________________________________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     “∵四边形ABCD是矩形，∴四边形ABCD的对角线相等．”以上推理的大前提是

    ________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    从1＝12,2＋3＋4＝32,3＋4＋5＋6＋7＝52中，可得到一般规律为

    ____________________________________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知下列三个方程：x2＋4ax－4a＋3＝0，x2＋(a－1)x＋a2＝0，x2＋2ax－2a＝0至少有一个方程有实数根，求实数a的取值范围．

    查看答案和解析>>

    同步练习册答案