
| A. | (2,$\frac{8}{3}$) | B. | ($\frac{2}{3}$,2) | C. | (2,$\frac{10}{3}$) | D. | ($\frac{4}{3}$,$\frac{8}{3}$) |
分析 根据对函数的解析式进行变形后发现当x∈(-1,1],[3,5],[7,9]时,f(x)的图象为半径为1的半圆.当x∈(1,3],[7,7],[9,11]时,f(x)的图象是等腰三角形,根据图象推断要使方程恰有5个实数解,则需直线y=$\frac{x}{3}$与前两个等腰三角形有两个交点,而与第三个等腰三角形不相交,由此可求得m的范围.
解答 解:∵当x∈(-1,1]时,将函数化为方程x2+y2=1(y≥0),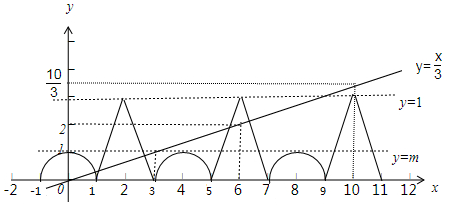
∴实质上为一个半径为1半圆,
其图象如图所示,
同时在坐标系中作出
当x∈(1,3]时,
y=m(1-|x-2|),
0≤1-|x-2|)<1的图象,
其图象为等腰三角形,
再根据周期性作出函数其它部分的图象,
当x∈(-1,1],[3,5],[7,9]时,f(x)的图象为半径为1的半圆.
当x∈(1,3],[7,7],[9,11]时,f(x)的图象是等腰三角形,
∵函数g(x)=3f(x)-x恰有5个不同零点,
∴需直线y=$\frac{x}{3}$与前两个等腰三角形有两个交点,而与第三个等腰三角形不相交
∴由图象知直线y=$\frac{x}{3}$与第一个等腰三角形有两个交点,与第二个等腰三角形没有交点,
∴2<m<$\frac{10}{3}$.
故选:C.
点评 本题考查的知识点是根的存在性及根的个数判断,及函数的周期性,其中根据方程根与函数零点的关系,结合函数解析式进行分析是解答本题的关键.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AA1=2,AC=$\sqrt{5}$,BC=3,M,N分别为B1C1,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
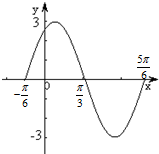 已知函数y=Asin(ωx+φ)(A>0,ω>0)|φ|<$\frac{π}{2}$的图象如图所示,
已知函数y=Asin(ωx+φ)(A>0,ω>0)|φ|<$\frac{π}{2}$的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
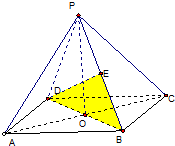 如图正方形ABCD中,O为中心,PO⊥面ABCD,E是PC中点,求证:
如图正方形ABCD中,O为中心,PO⊥面ABCD,E是PC中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{π}{24}$ | B. | x=$\frac{5π}{12}$ | C. | x=$\frac{π}{2}$ | D. | x=$\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com