Question

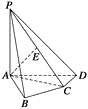
【题目】如图，在四棱锥P—ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC＝60°，PA＝AB＝BC，E是PC的中点.

(1) 证明：AE⊥平面PCD；

(2) 求PB和平面PAD所成的角的大小.

Answer 1

【答案】(1)详见解析(2) 45°.

【解析】试题分析：(1) 要证明AE⊥平面PCD，只要证明AE⊥PC，结合AE⊥CD，即可证明结论；(2) 求PB和平面PAD所成的角的大小，说明∠APB就是要求的角即可求解

试题解析：(1)证明 在四棱锥P—ABCD中，因为PA⊥底面ABCD，CD平面ABCD，

故CD⊥PA.…1分 由条件CD⊥AC，PA∩AC＝A，…2分 ∴CD⊥平面PAC.…3分

又AE平面PAC，∴AE⊥CD.…4分由PA＝AB＝BC，∠ABC＝60°，可得AC＝PA.…5分

∵E是PC的中点，∴AE⊥PC.…6分 又PC∩CD＝C，综上得AE⊥平面PCD.…7分

(2)在四棱锥P—ABCD中，因为PA⊥底面ABCD，AB平面ABCD，故PA⊥AB.…8分

又AB⊥AD，PA∩AD＝A，则 AB⊥平面PAD，…9分 故PB在平面PAD内的射影为PA，则∠APB为PB和平面PAD所成的角.……10分 在Rt△PAB中，AB＝PA，

故∠APB＝45°.…11分所以PB和平面PAD所成的角的大小为45°.……12分