
如图,三棱柱 中,所有棱长均为2,
中,所有棱长均为2,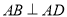 ,
,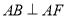 ,平面
,平面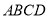 ⊥平面
⊥平面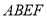 ,
,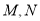 分别是
分别是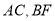 上的中点.
上的中点.

(1)求证: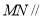 平面
平面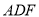 ;
;
(2)求直线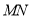 与平面
与平面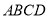 所成角的大小.
所成角的大小.
(1)证明见解析;(2)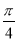
【解析】
试题分析:(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(3)空间向量将空间位置关系转化为向量运算,应用的核心是要充分认识形体特征,建立恰当的坐标系,实施几何问题代数化.同时注意两点:一是正确写出点、向量的坐标,准确运算;二是空间位置关系中判定定理与性质定理条件要完备.
试题解析:【解析】
(1)方法一:如图取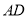 中点
中点 ,取
,取 中点
中点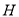 ,连结
,连结
则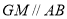 ,且
,且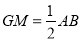 ,同理
,同理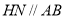 ,且
,且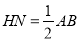
故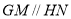 ,且
,且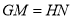
所以四边形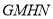 是平行四边形, 3分
是平行四边形, 3分
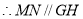 ,又
,又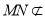 平面
平面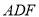 ,
,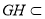 GH
GH 平面
平面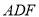
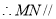 平面
平面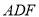 5分
5分
方法二:如图,取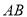 中点
中点 ,连结
,连结

则 ,又
,又 平面
平面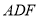 ,
,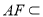 平面
平面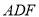
 平面
平面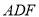 2分
2分
同理可证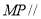 平面
平面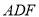 ,又
,又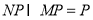
故平面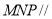 平面
平面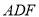 4分
4分
又 平面
平面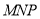
故 平面
平面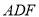 5分
5分
(2)方法一:如(1)方法二所示,取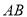 中点
中点 ,则
,则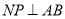 ,
,
又平面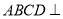 ⊥平面
⊥平面 ,且
,且 平面
平面 ,故
,故 平面
平面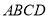 7分
7分
从而 在平面
在平面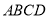 上的射影为
上的射影为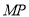 ,
,
故 就是直线
就是直线 与平面
与平面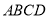 所成的角. 9分
所成的角. 9分
又
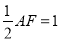 ,
,
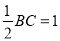 ,从而
,从而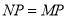
故 , 12分
, 12分
故直线 与平面
与平面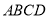 所成的角等于
所成的角等于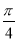 13分
13分
方法二:依题意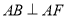 ,且
,且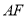
 平面
平面 ,平面
,平面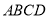 ⊥平面
⊥平面 ,故
,故 平面
平面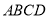
从而 ,又
,又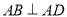 ,故分别以
,故分别以 所在直线为
所在直线为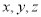 轴,建立空间直角坐标系. 7分
轴,建立空间直角坐标系. 7分
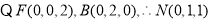 ,同理可得
,同理可得 故
故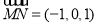 8分
8分
取平面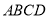 的法向量为
的法向量为 , 9分
, 9分
设直线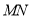 与平面
与平面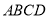 所成角为
所成角为
则 , 11分
, 11分
又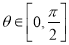
从而直线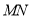 与平面
与平面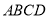 所成角为
所成角为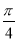 13分
13分
考点:1、直线与平面平行的判断;2、直线与平面所成的角;3、空间向量在立体几何的应用.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:高中数学 来源:2015届福建省高三10月月考理科数学试卷(解析版) 题型:解答题
(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系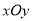 中,直线
中,直线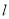 的参数方程为
的参数方程为 为参数),P、Q分别为直线
为参数),P、Q分别为直线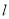 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线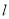 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,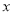 轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源:2015届福建省等三校高三上学期期中联考理科数学试卷(解析版) 题型:选择题
已知角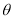 的顶点与原点重合,始边与
的顶点与原点重合,始边与 轴的非负半轴重合,终边上一点
轴的非负半轴重合,终边上一点 ,则
,则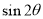 等于( )
等于( )
 B.
B.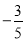 C.
C.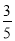 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届福建省、德化一中高三9月摸底考试理科数学试卷(解析版) 题型:填空题
某次测量发现一组数据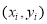 具有较强的相关性,并计算得
具有较强的相关性,并计算得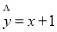 ,其中数据
,其中数据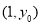 因书写不清,只记得
因书写不清,只记得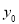 是
是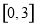 任意一个值,则该数据对应的残差的绝对值不大于1的概率为 .(残差=真实值-预测值.)
任意一个值,则该数据对应的残差的绝对值不大于1的概率为 .(残差=真实值-预测值.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com