


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
| a |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
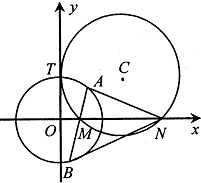 圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.
圆C与y轴切于点(0,2),与x轴正半轴交于两点M,N(点M在点N的左侧),且|MN|=3.查看答案和解析>>
科目:高中数学 来源: 题型:
 某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为
某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如图所示,则违规扣分的汽车大约为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com