
分析 推导出f(x)是偶函数,f(x)在(0,$\frac{2π}{3}$]上是增函数,从而f(x)图象类似于开口向上的抛物线,由此能求出结果.
解答 解:∵f(-x)=(-x)2-2cos(-x)=x2-2cosx=f(x),
∴f(x)是偶函数,
∴f(x)图象关于y轴对称.
∵f′(x)=2x+2sinx>0,x∈(0,$\frac{2π}{3}$],
∴f(x)在(0,$\frac{2π}{3}$]上是增函数.
∴f(x)图象类似于开口向上的抛物线,
∴若|x1|>|x2|,则f(x1)>f(x2),
∵x1>x2成立,|x1|>|x2|不一定成立,∴①是错误的.
∵x12>x22成立,|x1|>|x2|一定成立,∴②是正确的.
∵x1>|x2|成立,|x1|>|x2|一定成立,∴③是正确的.
故答案为:②③.
点评 本题考查满足题意的条件的选择,是中档题,解题时要认真审题,注意函数性质、导数性质的合理运用.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 实数k有最大值2 | B. | 实数k有最小值2 | C. | 实数k有最大值$\frac{2}{e}$ | D. | 实数k有最小值$\frac{2}{e}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
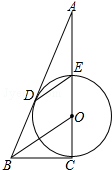 如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A
如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$i | D. | i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com