
分析 (1)由A${\;}_{n}^{3}$=6C${\;}_{n}^{4}$,则n(n-1)(n-2)=$6×\frac{n(n-1)(n-2)(n-3)}{4×3×2×1}$,n≥4,解得n=7,即可判断出正误;
(2)举反例,如${∫}_{0}^{\frac{3π}{2}}sinxdx$>0,当x∈$(π,\frac{3π}{2})$时,sinx<0;
(3)举反例,如f(x)=x3,f′(x)=3x2,f′(0)=0,而x=0不是函数f(x)的极值点;
(4)设z=x+yi,x,y∈R,由|z+2-2i|=1,可得(x+2)2+(y-2)2=1,圆心C(-2,2),则|OC|=2$\sqrt{2}$,则|z|的最小值=|OC|-1,即可判断出正误.
解答 解:(1)若A${\;}_{n}^{3}$=6C${\;}_{n}^{4}$,则n(n-1)(n-2)=$6×\frac{n(n-1)(n-2)(n-3)}{4×3×2×1}$,n≥4,化为4=n-3,解得n=7,因此正确;
(2)若${∫}_{b}^{a}$f(x)dx>0,则f(x)>0,不正确,例如${∫}_{0}^{\frac{3π}{2}}sinxdx$>0,当x∈$(π,\frac{3π}{2})$时,sinx<0;
(3)导数为零的点不一定是极值点,例如f(x)=x3,f′(x)=3x2,f′(0)=0,而x=0不是函数f(x)的极值点;
(4)若z∈C,设z=x+yi,x,y∈R,由|z+2-2i|=1,可得(x+2)2+(y-2)2=1,圆心C(-2,2),则|OC|=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,∴则|z|的最小值=|OC|-1=2$\sqrt{2}$-1,正确.
其中正确的命题序号为 (1)(4).
故答案为:(1)(4).
点评 本题考查了易逻辑的判定方法、排列与组合数计算公式、微积分基本定理性质、函数导数与极值点的关系、复数的运算性质、圆的性质,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1.99 | 3 | 4 | 5.1 | 6.12 |
| y | 1.5 | 4.04 | 7.5 | 12 | 18.01 |
| A. | y=2x-2 | B. | y=$\frac{1}{2}$(x2-1) | C. | y=log2x | D. | y=${(\frac{1}{2})^x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
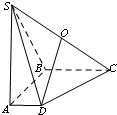 如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.
如图,在四棱锥S-ABCD中,底面ABCD是直角梯形,AB⊥AD,AB⊥BC,侧棱SA⊥底面ABCD,点O为侧棱SC的中点,且SA=AB=BC=2,AD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com