练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知函数f（x）=$\left\{\begin{array}{l}{x+a，x≤1}\\{\frac{x-1}{x+1}，x＞1}\end{array}\right.$，问a为何值时，$\underset{lim}{x→1}$f（x）存在．

    分析 f（x）在x=1处有定义，从而当$\underset{lim}{x→1}\frac{x-1}{x+1}=f（1）$时极限$\underset{lim}{x→1}f（x）$才存在，这样便可求出a．

    解答 解：$若\underset{lim}{x→1}f（x）$存在，则：$\underset{lim}{x→1}\frac{x-1}{x+1}=0=f（1）=1+a$；
    ∴a=-1；
    即a=-1时，$\underset{lim}{x→1}f（x）$存在．

    点评 考查函数极限的概念，分段函数极限的求法，清楚极限$\underset{lim}{x→{x}_{0}}f（x）$存在的充要条件．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

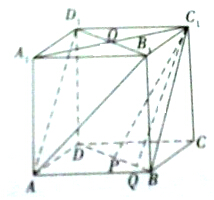    3．已知正方体ABCD-A1B1C1D1．
    （1）点P是BD的中点．求证：C1P∥平面AB1D1；
    （2）若点Q是BD上的一个动点，C1Q与平面AB1D1 是否平行？为什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知直线l1：3x+y-2=0与直线l2：mx-y+1=0的夹角为45°，则实数m=2或-$\frac{1}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知F1，F2分别为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，点P在椭圆上，△POF2是面积为$\sqrt{3}$的正三角形，则椭圆方程为$\frac{{x}^{2}}{4+2\sqrt{3}}$+$\frac{{y}^{2}}{2\sqrt{3}}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．关于x的方程x2+px+q=0和x2+qx+p=0都有两个不相等的实数根，且它们有且仅有一个公共根，则其余两个不同根之和为 （　　）
    A．1B．-1C．p+qD．-p-q

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知点P1（x0，y0）为双曲线$\frac{{x}^{2}}{8{b}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（b为正常数）上任一点，F2为双曲线的右焦点，过P作直线x=$\frac{8b}{3}$的垂线，垂足为A，连接F2A并延长交y轴于P2．
    （1）求线段P1P2的中点P的轨迹E的方程；
    （2）设轨迹E与x轴交于B、D两点，在E上任取一点Q（x1，y1）（y1≠0），直线QB，QD分别交y轴于M，N两点．求证：以MN为直径的圆过两定点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=mx-1，g（x）=x2-2mx+m
    （1）m=1时，求g（x）的单调增区间；
    （2）记函数G（x）=g（x）+f（x）
    ①若函数y=|G（x）|在[2，4]上单调递增，求实数m的范围；
    ②是否存在整数a，b，使得关于x的不等式a≤G（x）≤b的解集为[a，b]，若存在求出a，b的值，若不存在请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知cos（$\frac{π}{6}$-α）=$\frac{2}{3}$，则sin（$\frac{2π}{3}$-α）=$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．给出以下命题：
    （1）若A${\;}_{n}^{3}$=6C${\;}_{n}^{4}$，则n的值为7；
    （2）若${∫}_{b}^{a}$f（x）dx＞0，则f（x）＞0；
    （3）导数为零的点一定是极值点；
    （4）若z∈C，且|z+2-2i|=1，则|z|的最小值是2$\sqrt{2}$-1；
    其中正确的命题序号为（1）（4）．

    查看答案和解析>>

    同步练习册答案