
【题目】设函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若![]() ,证明
,证明![]() 恒成立.
恒成立.
【答案】(1)当![]() 时,
时,![]() 在区间
在区间![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增;(2)证明见详解.
上单调递增;(2)证明见详解.
【解析】
(1)求导,对参数进行分类讨论,进而求得函数的单调区间;
(2)将恒成立问题,转化两个函数最值之间的问题,进而求解.
(1)由题意得![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,故函数
,故函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
②当![]() 时,在区间
时,在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上,
上,![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增.
上单调递增.
(2)证明:
要证![]() ,只需证
,只需证![]() .
.
又![]() ,故只需证
,故只需证![]() 即可.
即可.
设![]() ,则
,则![]() ,
,
在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上,
上,![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以![]() .
.
设![]() ,则
,则![]() ,
,
在区间![]() 上,
上,![]() ,在区间
,在区间![]() 上,
上,![]() ,
,
故函数![]() 在区间
在区间![]() 上单调递增,在区间
上单调递增,在区间![]() 上单调递减,
上单调递减,
所以![]() .
.
又![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
故在![]() 上,
上,![]() ,
,
综上,![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】在平行六面体ABCD﹣A1B1C1D1中,所有棱长均为2,∠AA1D1=∠AA1B1=60°,∠D1A1B1=90°.
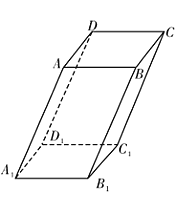
(1)求证:A1C⊥B1D1;
(2)求对角线AC1的长;
(3)求二面角C1﹣AB1﹣D1的平面角的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词,寻文化基因,品生活之美”为宗旨.每一期的比赛包含以下环节:“个人追逐赛”、“攻擂资格争夺赛”和“擂主争霸赛”,其中“擂主争霸赛”由“攻擂资格争夺赛”获胜者与上一场擂主进行比拼.“擂主争霸赛”共有九道抢答题,抢到并答对者得一分,答错则对方得一分,率先获得五分者即为该场擂主.在《中国诗词大会》的某一期节目中,若进行“擂主争霸赛”的甲乙两位选手每道抢答题得到一分的概率都是为0.5,则抢答完七道题后甲成为擂主的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,(其中
,(其中![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() ……).
……).
(1)令![]() ,若
,若![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的值;
的值;
(2)在(1)的条件下,设![]() 为整数,且对于任意正整数
为整数,且对于任意正整数![]() ,
, ![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为![]() (
(![]() 为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线
为参数).以坐标原点O为极,z轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线C的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设点![]() .若直线
.若直线![]() 与曲线C相交于A,B两点,求
与曲线C相交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(1)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(2)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.用X表示抽取的3人中睡眠充足的员工人数,求随机变量X的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com