
分析 (1)利用两角和差的正切公式进行化简求解即可.
(2)利用向量数量积的定义以及向量模长与向量数量积的关系进行转化,转化为三角函数进行求解即可.
解答 解:(1)∵$\sqrt{3}$(tanA-tanB)=1+tanA•tanB,又△ABC为锐角三角形
∴$\frac{tanA-tanB}{1+tanAtanB}$=$\frac{\sqrt{3}}{3}$,即tan(A-B)=$\frac{tanA-tanB}{1+tanAtanB}$=$\frac{\sqrt{3}}{3}$,
∵0<A<$\frac{π}{2}$,0<B<$\frac{π}{2}$,
∴-$\frac{π}{2}$<A-B<$\frac{π}{2}$,
则A-B=$\frac{π}{6}$.
(2)∵$\overrightarrow{m}$=(sinA,cosA),$\overrightarrow{n}$=(cosB,sinB),
∴|$\overrightarrow{m}$|=1,|$\overrightarrow{n}$|=1,$\overrightarrow{m}$•$\overrightarrow{n}$=sinAcosB+cosAsinB=sin(A+B),
则|3$\overrightarrow{m}$-2$\overrightarrow{n}$|2=9|$\overrightarrow{m}$|2+4|$\overrightarrow{n}$|2-12$\overrightarrow{m}$•$\overrightarrow{n}$=13-12sin(A+B)=13-12sin(2B+$\frac{π}{6}$),
∵$\frac{π}{6}$<B<$\frac{π}{3}$,∴$\frac{π}{2}$<2B+$\frac{π}{6}$<$\frac{5π}{6}$,
∴sin(2B+$\frac{π}{6}$)∈($\frac{1}{2}$,1),12sin(2B+$\frac{π}{6}$)∈(6,12),13-12sin(2B+$\frac{π}{6}$)∈(1,7),
则|3$\overrightarrow{m}$-2$\overrightarrow{n}$|∈(1,$\sqrt{7}$)
∴|3$\overrightarrow{m}$-2$\overrightarrow{n}$|的取值范围是(1,$\sqrt{7}$).
点评 本题主要考查两角和差的正切公式以及向量数量积与三角函数的综合,利用向量模长与向量数量积的关系转化为三角函数是解决本题的关键.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{OA}$,$\overrightarrow{BC}$ | B. | $\overrightarrow{OA}$,$\overrightarrow{CD}$ | C. | $\overrightarrow{AB}$,$\overrightarrow{CF}$ | D. | $\overrightarrow{AB}$,$\overrightarrow{DE}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
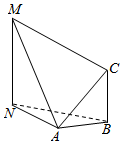 如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从M点测得A点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°;已知山高BC=200m,则山高MN=( )
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从M点测得A点的俯角∠NMA=30°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°;已知山高BC=200m,则山高MN=( )| A. | 300 m | B. | 200$\sqrt{2}$ m | C. | 200$\sqrt{3}$ m | D. | 300$\sqrt{2}$ m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com