
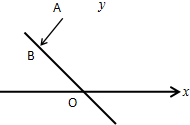
分析 根据题意设点A(x0,y0),过A作y=-x的垂线,垂足B(x1,y1),就是A的映射,求得AB的方程,将y=x-代入直线方程,求得x1和y1,将其写成矩阵乘积的形式,即可求得矩阵M.
解答 解:设点A(x0,y0),过A作y=-x的垂线,垂足B(x1,y1),就是A的映射,
AB的斜率1,方程y-y0=(x-x0)=x-x0,
y=-x代入:-x-y0=x-x0,整理得:2x=x0-y0,x1=$\frac{1}{2}$(x0-y0)
y1=-x1=-$\frac{1}{2}$(x0-y0)
∴垂直投影到直线y=-x上的投影变换矩阵M=$[\begin{array}{l}{\frac{1}{2}}&{-\frac{1}{2}}\\{-\frac{1}{2}}&{\frac{1}{2}}\end{array}]$.
点评 本题考查矩阵变换及矩阵投影变换,考查分析问题及计算能力,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:解答题
| 不常吃零食 | 常吃零食 | 总计 | |
| 不患龋齿 | |||
| 患龋齿 | |||
| 总计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
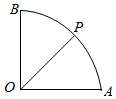 扇形OAB中,∠AOB=90°,OA=2,其中C是OA的中点,P是$\widehat{AB}$上的动点(含端点),若实数λ,μ满足$\overrightarrow{OP}$=λ$\overrightarrow{OC}$+μ$\overrightarrow{OB}$,则λ+μ的取值范围是( )
扇形OAB中,∠AOB=90°,OA=2,其中C是OA的中点,P是$\widehat{AB}$上的动点(含端点),若实数λ,μ满足$\overrightarrow{OP}$=λ$\overrightarrow{OC}$+μ$\overrightarrow{OB}$,则λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [1,$\sqrt{3}$] | C. | [1,2] | D. | [1,$\sqrt{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com