
【题目】已知向量 ![]() =(cosx,﹣
=(cosx,﹣ ![]() ),
), ![]() =(
=( ![]() sinx,cos2x),x∈R,设函数f(x)=
sinx,cos2x),x∈R,设函数f(x)= ![]() .
.
(1)求f(x)的最小正周期.
(2)求f(x)在[0, ![]() ]上的最大值和最小值.
]上的最大值和最小值.
【答案】
(1)解:函数f(x)= ![]() =(cosx,﹣
=(cosx,﹣ ![]() )(
)( ![]() sinx,cos2x)
sinx,cos2x)
= ![]() sinxcosx
sinxcosx ![]()
=sin(2x﹣ ![]() )
)
最小正周期为:T= ![]() =π.
=π.
(2)解:当x∈[0, ![]() ]时,2x﹣
]时,2x﹣ ![]() ∈
∈ ![]() ,
,
由正弦函数y=sinx在 ![]() 的性质可知,sinx
的性质可知,sinx ![]() ,
,
∴sin(2x﹣ ![]() )
) ![]() ,
,
∴f(x)∈[﹣ ![]() ,1],
,1],
所以函数f(x)在[0, ![]() ]上的最大值和最小值分别为:1,﹣
]上的最大值和最小值分别为:1,﹣ ![]() .
.
【解析】(1)通过向量的数量积以及二倍角的正弦函数两角和的正弦函数,化简函数为一个角的一个三角函数的形式,通过周期公式,求f(x)的最小正周期.(2)通过x在[0, ![]() ],求出f(x)的相位的范围,利用正弦函数的最值求解所求函数的最大值和最小值.
],求出f(x)的相位的范围,利用正弦函数的最值求解所求函数的最大值和最小值.
【考点精析】本题主要考查了两角和与差的正弦公式和三角函数的最值的相关知识点,需要掌握两角和与差的正弦公式:![]() ;函数
;函数![]() ,当
,当![]() 时,取得最小值为
时,取得最小值为![]() ;当
;当![]() 时,取得最大值为
时,取得最大值为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在xOy平面上,将两个半圆弧(x﹣1)2+y2=1(x≥1)和(x﹣3)2+y2=1(x≥3),两条直线y=1和y=﹣1围成的封闭图形记为D,如图中阴影部分,记D绕y轴旋转一周而成的几何体为Ω.过(0,y)(|y|≤1)作Ω的水平截面,所得截面积为4π ![]() +8π.试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为 .
+8π.试利用祖暅原理、一个平放的圆柱和一个长方体,得出Ω的体积值为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的一个顶点为A(2,0),离心率为
(a>b>0)的一个顶点为A(2,0),离心率为![]() .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为![]() 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2016年6月英国“脱欧”公投前夕,为了统计该国公民是否有“留欧”意愿,该国某中学数学兴趣小组随机抽查了50名不同年龄层次的公民,调查统计他们是赞成“留欧”还是反对“留欧”.现已得知50人中赞成“留欧”的占60%,统计情况如下表:
年龄层次 | 赞成“留欧” | 反对“留欧” | 合计 |
18岁—19岁 | 6 | ||
50岁及50岁以上 | 10 | ||
合计 | 50 |
(1)请补充完整上述列联表;
(2)请问是否有97.5%的把握认为赞成“留欧”与年龄层次有关?请说明理由.
参考公式与数据: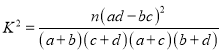 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班运动队由足球运动员18人,篮球运动员12人、羽毛球运动员6人组成(每人只参加一项),现从这些运动员中抽取个容量为![]() 的样本,若分别采用系统抽样法和分层抽样法,则都不用剔除个体;当抽取样本的容量为
的样本,若分别采用系统抽样法和分层抽样法,则都不用剔除个体;当抽取样本的容量为![]() 时,若采用系统抽样法,则需要剔除一个个体,则样本容量
时,若采用系统抽样法,则需要剔除一个个体,则样本容量![]() ( )
( )
A. 6B. 7C. 12D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ![]() ,底面是边长为
,底面是边长为 ![]() 的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aex,g(x)=lnx-lna,其中a为常数,且曲线y=f(x)在其与y轴的交点处的切线记为l1,曲线y=g(x)在其与x轴的交点处的切线记为l2,且l1∥l2.
(1)求l1,l2之间的距离;
(2)若存在x使不等式![]() 成立,求实数m的取值范围;
成立,求实数m的取值范围;
(3)对于函数f(x)和g(x)的公共定义域中的任意实数x0,称|f(x0)-g(x0)|的值为两函数在x0处的偏差.求证:函数f(x)和g(x)在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com