
| A. | ①②③ | B. | ②③④ | C. | ③④ | D. | ②④ |
分析 根据已知中g(k)表示k的最大奇数因数,Sn=g(1)+g(2)+g(3)+…+g(2n).逐一分析四个结论的真假,可得答案.
解答 解:∵g(k)表示k的最大奇数因数,Sn=g(1)+g(2)+g(3)+…+g(2n).
∴①g(3)+g(4)=3+1=4≠10,故错误;
②?m∈N*,都有g(2m)=g(m),故正确;
③S1+S2+S3=(1+1)+(1+1+3+1)+(1+1+3+1+5+3+7+1)=30,故正确;
④当n≥2时,Sn=g(1)+g(2)+g(3)+g(4)+…+g(2n-1)+g(2n)
=[g(1)+g(3)+g(5)+…+g(2n-1)]+[g(2)+g(4)+…+g(2n)]
=[1+3+5+…+(2n-1)]+[g(2×1)+g(2×2)+…+g(2×2n-1)]
=$\frac{(1+{2}^{n}-1)×{2}^{n-1}}{2}$+[g(1)+g(2)+…+g(2n-1)]=4n-1+Sn-1,
于是Sn-Sn-1=4n-1,n≥2,n∈N*.故正确;
故选:B
点评 本题考查新定义,考查数列的求和,解题的关键是正确理解新定义,正确求数列的和是关键.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,0) | C. | $({\frac{1}{3},1})$ | D. | (2.+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2] | B. | (1,+∞) | C. | (2,+∞) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
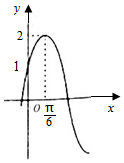
| A. | f(x)=2sin3x | B. | $f(x)=2sin(x+\frac{π}{3})$ | C. | $f(x)=2sin(3x+\frac{π}{6})$ | D. | $f(x)=2sin(2x+\frac{π}{6})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com