
分析 根据题意,由余弦定理可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,将其代入bcosC+ccosB中计算可得答案.
解答 解:根据题意,△ABC中,由余弦定理可得cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
bcosC+ccosB=b×$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$+c×$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=a=$\sqrt{3}$,
即bcosC+ccosB=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查余弦定理的运用,解题的关键是正确利用余弦定理.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的最小正周期为π | B. | f(x)在区间$[{0,\frac{π}{2}}]$上是增函数 | ||
| C. | f(x)的图象关于点$({-\frac{3π}{4},0})$对称 | D. | f(x)的图象关于直线$x=\frac{5π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
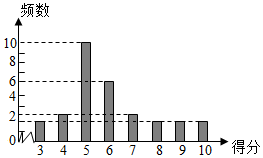 为了普及环保知识,增强环保意识,随机抽取某大学30民学生参加环保知识测试,得分(10分制)如图所示,假设得分的中位数为me,众数为mσ,平均数为$\overline{x}$,则me,mσ,$\overline{x}$之间的大小关系是mσ<me<$\overline{x}$.
为了普及环保知识,增强环保意识,随机抽取某大学30民学生参加环保知识测试,得分(10分制)如图所示,假设得分的中位数为me,众数为mσ,平均数为$\overline{x}$,则me,mσ,$\overline{x}$之间的大小关系是mσ<me<$\overline{x}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com