Question

14．在△ABC中，角A，B，C所对的边分别为a，b，c，已知B=60°，a+c=4．
（1）当a，b，c成等差数列时，求△ABC的面积；
（2）设D为AC边的中点，求线段BD长的最小值．

Answer 1

分析 （1）由已知利用等差数列的性质可求b=2，由余弦定理可得ac=4，利用三角形面积公式即可求值得解．
（2）设AD=CD=d，由cos∠ADB+cos∠CDB=0，结合余弦定理可得BD²=$\frac{{a}^{2}+{c}^{2}}{2}$-d²=8-ac-d²，又利用余弦定理可得4d²=16-3ac，从而解得d²=4-$\frac{3ac}{4}$，利用基本不等式可得：BD²=4-$\frac{ac}{4}$≥4-$\frac{1}{4}$（$\frac{a+c}{2}$）²=3，即可得解．

解答 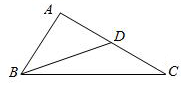解：（1）因为a，b，c成等差数列，a+c=4．
所以b=$\frac{a+c}{2}$=2，…（2分）
由余弦定理，得b²=a²+c²-2accosB=（a+c）²-3ac=16-3ac=4，解得ac=4，…（6分
从而S_△ABC=$\frac{1}{2}$acsinB=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$．…（8分）⇒
（2）因为D为AC边的中点，所以可设AD=CD=d，
由cos∠ADB+cos∠CDB=0，得$\frac{B{D}^{2}+{d}^{2}-{c}^{2}}{2d•BD}$+$\frac{B{D}^{2}+{d}^{2}-{a}^{2}}{2d•BD}$=0，
即BD²=$\frac{{a}^{2}+{c}^{2}}{2}$-d²=8-ac-d²，…（10分）
又因为b²=a²+c²-2accosB=（a+c）²-3ac=16-3ac，
即4d²=16-3ac，
所以d²=4-$\frac{3ac}{4}$，…（12分）
故BD²=4-$\frac{ac}{4}$≥4-$\frac{1}{4}$（$\frac{a+c}{2}$）²=3，当且仅当a=c时取等号，
所以线段BD长的最小值为$\sqrt{3}$．…（14分）

点评 本题主要考查了等差数列的性质，余弦定理，三角形面积公式，基本不等式在解三角形中的应用，考查了计算能力和转化思想，属于中档题．