
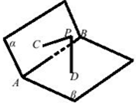
 如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:
如图,已知二面角α-AB-β的大小为120°,PC⊥α,PD⊥β,C、D是垂足,C、D不在直线AB上,PC=PD=$\sqrt{3}$,有如下命题:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 如图所示,设平面PCD与AB相交于点Q,连接CQ,QD.由于PC⊥α,PD⊥β,α∩β=AB.可得PC⊥AB,PD⊥AB,AB⊥CQ,AB⊥QD,于是∠CQD是二面角α-AB-β的平面角,大小为120°.即可判断出正误.
解答 解:如图所示,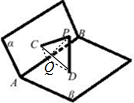
设平面PCD与AB相交于点Q,连接CQ,QD.
∵PC⊥α,PD⊥β,α∩β=AB.
∴PC⊥AB,PD⊥AB,
∴AB⊥平面PCQD.
∴AB⊥CQ,AB⊥QD,
∴∠CQD是二面角α-AB-β的平面角,大小为120°.
因此:直线AB与直线CD是异面直线;直线AB与直线CD垂直;∠CPD=60°;由PC=PD=$\sqrt{3}$,可得点P到直线AB的距离是2.
其中正确命题的个数是4.
故选:D.
点评 本题考查了空间位置关系及其空间角,考查了推理能力与计算能力,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 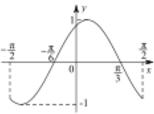 | B. | 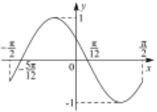 | ||
| C. | 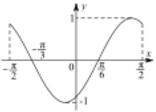 | D. | 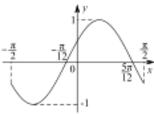 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com