
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据平面向量的基本概念,对选项中的命题进行分析、判断正误即可.
解答 解:对于①,单位向量的大小相等相等,但方向不一定相同,故①错误;
对于②,模相等的两个平行向量是相等向量或相反向量,故②错误;
对于③,向量是有方向的量,不能比较大小,故③错误;
对于④,向量是可以平移的矢量,当两个向量相等时,
它们的起点和终点不一定相同,故④错误;
对于⑤,$\overrightarrow{b}$=$\overrightarrow{0}$时,$\overrightarrow{a}$∥$\overrightarrow{b}$,$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$与$\overrightarrow{c}$不一定平行.
综上,以上正确的命题个数是0.
故选:A.
点评 本题考查了平面向量的基本概念与应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
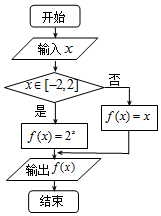
| A. | [1,4] | B. | [-1,4] | C. | [-1,1]∪[2,4] | D. | [0,1]∪(2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数y=sin2a+$\frac{4}{si{n}^{2}a}$的最小值是4 | B. | $\sqrt{6}$+$\sqrt{11}$>$\sqrt{3}$+$\sqrt{14}$ | ||
| C. | 函数y=sina+$\frac{1}{sina}$的最小值是2 | D. | 58>312 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com