
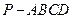 中,底面
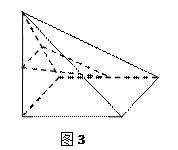
中,底面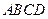 为正方形,
为正方形, 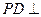 平面
平面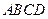 ,
,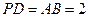 ,
,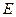 ,
,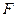 ,
,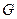 分别为
分别为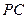 、
、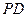 、
、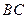 的中点.
的中点.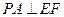 ;
;
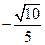
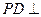 平面
平面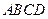 ,
,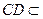 平面
平面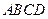 ,∴
,∴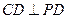 .
.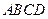 为正方形,∴
为正方形,∴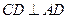 .
.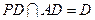 ,∴
,∴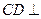 平面
平面 .……………………………………………3分
.……………………………………………3分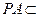 平面
平面 ,∴
,∴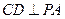 .
.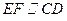 ,∴
,∴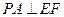 .…………………………………………………………6分
.…………………………………………………………6分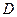 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系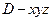 ,则
,则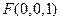 ,
,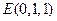
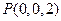 ,
,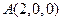 ,
,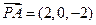 ,
,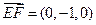 .………4分
.………4分 ,∴
,∴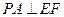 .………6分
.………6分
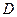 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系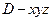 ,
,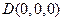 ,
,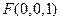 ,
,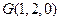 ,
,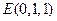 ,
, 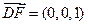 ,
,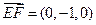 ,……………8分
,……………8分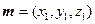 ,
,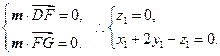
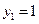 ,得
,得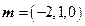 是平面
是平面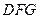 的一个法向量.…………………………10分
的一个法向量.…………………………10分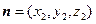 ,
,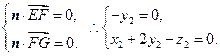
 ,得
,得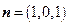 是平面
是平面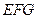 的一个法向量.……………………………12分
的一个法向量.……………………………12分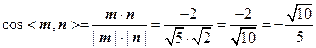 .
.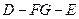 的平面角为θ,则
的平面角为θ,则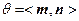 .
.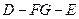 的余弦值为
的余弦值为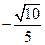 .………………………………………14分
.………………………………………14分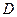 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系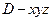 ,W
,W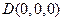 ,
,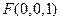 ,
,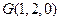 ,
,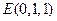 ,
,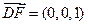 ,
,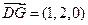
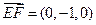 ,
,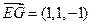 ,
,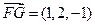 .………………………………8分
.………………………………8分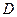 作
作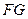 的垂线,垂足为
的垂线,垂足为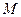 ,
,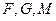 三点共线,∴
三点共线,∴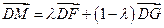 ,
,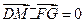 ,∴
,∴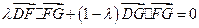 ,
,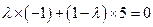 ,解得
,解得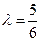 .
. .………………………………………………10分
.………………………………………………10分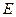 作
作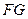 的垂线,垂足为
的垂线,垂足为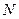 ,
,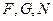 三点共线,∴
三点共线,∴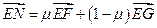 ,
,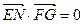 ,∴
,∴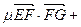
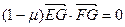 ,
, ,解得
,解得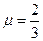 .
.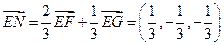 .……………………………………………12分
.……………………………………………12分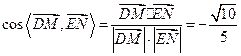 .
.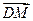 与
与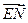 所成的角就是二面角
所成的角就是二面角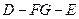 的平面角,
的平面角,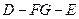 的余弦值为
的余弦值为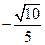 .………………………………………14分
.………………………………………14分


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题



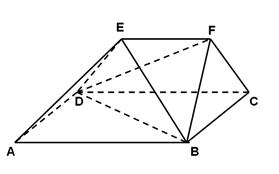
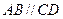 ,
,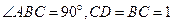 ,AB=2,E为AB的中点,将
,AB=2,E为AB的中点,将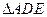 沿DE翻折至
沿DE翻折至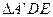 ,使二面角A
,使二面角A
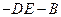 为直二面角。
为直二面角。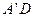 、
、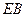 的中点,求证:
的中点,求证: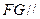 平面
平面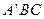 ;
; 度数的余弦值
度数的余弦值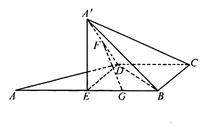
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com