
| A. | $y=3sin\frac{π}{6}t+12$ | B. | $y=-3sin\frac{π}{6}t+12$ | C. | $y=3sin\frac{π}{12}t+12$ | D. | $y=3cos\frac{π}{12}t+12$ |
分析 高潮时水深为A+K,低潮时水深为-A+K,联立方程组求得A和K的值,再由相邻两次高潮发生的时间相距12h,可知周期为12,由此求得ω值,再结合t=3时涨潮到一次高潮,把点(3,15)代入y=Asin(ωx+φ)+K的解析式求得φ,则函数y=f(t)的表达式可求.
解答 解:依题意,$\left\{\begin{array}{l}{A+K=15}\\{-A+K=9}\end{array}\right.$,解得$\left\{\begin{array}{l}{A=3}\\{K=12}\end{array}\right.$,
又T=$\frac{2π}{ω}=12$,
∴ω=$\frac{π}{6}$.
又f(3)=15,
∴3sin($\frac{3}{6}π$+φ)+12=15,
∴sin($\frac{π}{2}$+φ)=1.
∴φ=0,
∴y=f(t)=3sin$\frac{π}{6}$t+12.
故选:A.
点评 本题是应用题,考查y=Asin(ωx+φ)+K型函数的图象和性质,关键是对题意的理解,是中档题.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
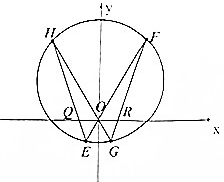 已知圆C的周长被y轴平分,且经过点A($\sqrt{3}$,0),B(0,3).
已知圆C的周长被y轴平分,且经过点A($\sqrt{3}$,0),B(0,3).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | 1 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
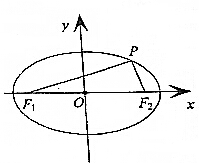 己知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为6,焦点F1(-c,0)到长轴的两个端点的距离之比为$\frac{1}{9}$.
己知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的短轴长为6,焦点F1(-c,0)到长轴的两个端点的距离之比为$\frac{1}{9}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com