
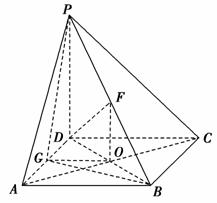
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,F是PB的中点.
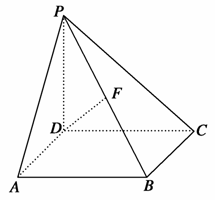
(1)求证:DF⊥AP.
(2)在线段AD上是否存在点G,使GF⊥平面PBC?若存在,说明G点的位置,并证明你的结论;若不存在,说明理由.
[证明] (1)取AB的中点E,则PA∥EF.设PD=DC=a,易求得DE=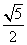 a,FE=
a,FE=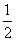 PA=
PA=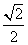 a,DF=
a,DF=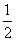 PB=
PB=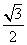 a.
a.
由于DE2=EF2+DF2,故DF⊥EF,
又EF∥PA,∴DF⊥PA.
(2)在线段AD上存在点G,使GF⊥平面PBC,且G点是AD的中点.
取AD的中点G,连接PG、BG,则PG=BG.又F为AB的中点,故GF⊥PB.
∵F为PB中点,
∴F点在底面ABCD上的射影为正方形ABCD的中心O,
∴FO⊥平面ABCD,∵BC⊂平面ABCD,∴FO⊥BC.
∵G为AD中点,O为正方形ABCD中心,∴GO⊥BC,
又GO∩FO=0,∴BC⊥平面GOF,∴GF⊥BC.
∵BC、PB是平面PBC内的两条相交直线,
∴GF⊥平面PBC.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
(2013·北京丰台期末)如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥BC,点M,N分别为A1C1与A1B的中点.
(1)求证:MN∥平面BCC1B1;
(2)求证:平面A1BC⊥平面A1ABB1.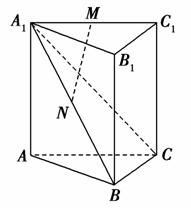
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=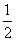 BC.
BC.
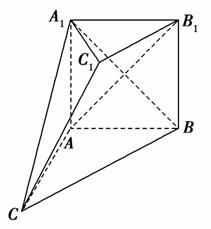
(1)求证:平面A1AC⊥平面ABC;
(2)求证:AB1∥平面A1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
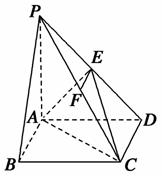
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD为长方形,AD=2AB,点E、F分别是线段PD、PC的中点.
(1)证明:EF∥平面PAB;
(2)在线段AD上是否存在一点O,使得BO⊥平面PAC,若存在,请指出点O的位置,并证明BO⊥平面PAC;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
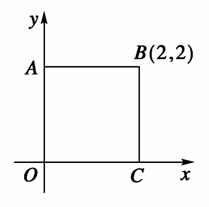
上图为水平放置的正方形ABCO,它在直角坐标系xOy中点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为( )
A.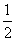 B.
B.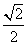
C.1 D.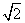
查看答案和解析>>
科目:高中数学 来源: 题型:
若直线l不平行于平面α,且l⃘α,则( )
A.α内的所有直线与l异面
B.α内不存在与l平行的直线
C.α内存在唯一的直线与l平行
D.α内的直线与l都相交
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
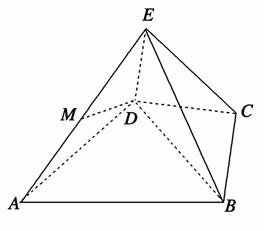
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com