
分析 (Ⅰ)利用两角和与差的三角函数以及二倍角公式化简函数的解析式,通过正弦函数的单调增区间求解即可.
(Ⅱ)利用三角函数的变换,求出函数的解析式,然后结合x的范围,求解函数的值域即可.
解答 解:(Ⅰ)函数f(x)=2sin($\frac{π}{4}$-x)•sin($\frac{π}{4}$+x)-2$\sqrt{3}$sinxcos(π-x)
=cos2x+$\sqrt{3}$sin2x=2sin(2x+$\frac{π}{6}$).
由2k$π-\frac{π}{2}$$≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$,k∈Z,
可得f(x)的单调递增区间为[k$π-\frac{π}{3}$,k$π+\frac{π}{6}$]k∈Z.
(Ⅱ)由(Ⅰ)可知f(x)=2sin(2x+$\frac{π}{6}$).函数y=f(x)的图象向左平移$\frac{π}{12}$个单位长度,
得到y=2sin(2(x+$\frac{π}{12}$)+$\frac{π}{6}$)=2sin(2x+$\frac{π}{3}$),
再将所得图象上各点的横坐标变为原来的2倍,纵坐标不变,得到函数y=g(x)=2sin(x+$\frac{π}{3}$)的图象,
x∈[0,$\frac{5π}{6}$],x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{7π}{6}$],故g(x)∈[-1,2].g(x)在[0,$\frac{5π}{6}$]上的值域为:[-1,2].
点评 本题考查三角函数的变换,三角函数的化简求值,恒等变换的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,$AB=\sqrt{2},AF=1$,M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{7}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
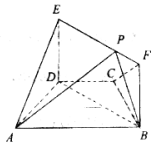 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
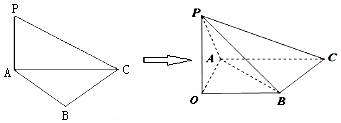
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
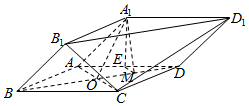 由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,
由四棱柱ABCD-A1B1C1D1截去三棱锥C1-B1CD1后得到的几何体如图所示,四边形ABCD为正方形,O为AC与BD 的交点,E为AD的中点,A1E⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 5 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com