
(已知抛物线 (
(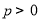 )的准线与
)的准线与 轴交于点
轴交于点 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线 (直线与抛物线交于点
(直线与抛物线交于点 ,
, ),使得三角形
),使得三角形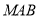 的面积
的面积 ?若存在,请求出直线
?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)参考解析;(2)存在,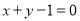 或
或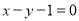
【解析】
试题分析:(1)由抛物线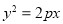 (
(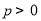 )的准线与
)的准线与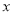 轴交于点
轴交于点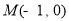 ,可求得
,可求得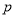 的值,即可得到抛物线方程与焦点坐标
的值,即可得到抛物线方程与焦点坐标
(2)由于过焦点的直线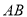 可能垂直于x轴,依题意不可能垂直于y轴,所以假设直线
可能垂直于x轴,依题意不可能垂直于y轴,所以假设直线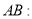
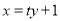 .再联立抛物线方程,由韦达定理以及弦长公式即可得到AB的弦长.由点到直线的距离公式即可得到点M到直线AB的距离.再由
.再联立抛物线方程,由韦达定理以及弦长公式即可得到AB的弦长.由点到直线的距离公式即可得到点M到直线AB的距离.再由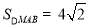 即可求出结论.
即可求出结论.
解法一:(1)由已知得: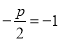 ,从而抛物线方程为
,从而抛物线方程为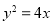 ,
,
焦点坐标为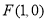 . 4分
. 4分
(2)由题意,设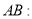
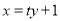 ,并与
,并与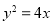 联立,
联立,
得到方程: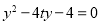 , 6分
, 6分
设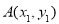 ,
, ,则
,则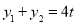 ,
, . 7分
. 7分
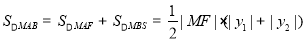
∵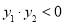 ,∴
,∴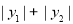
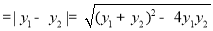
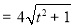 , 9分
, 9分
又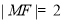 ,∴
,∴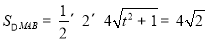 10分
10分
解得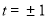 , 11分
, 11分
故直线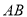 的方程为:
的方程为: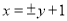 .即
.即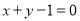 或
或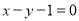 . 12分
. 12分
解法二:(1)(同解法一)
(2)当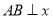 轴时,
轴时,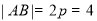 ,
,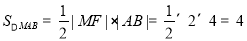 ,
,
不符合题意. 5分
故设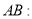
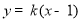 (
(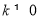 ),并与
),并与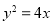 联立,
联立,
得到方程: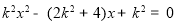 , 6分
, 6分
设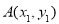 ,
, ,则
,则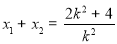 ,
,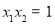 . 7分
. 7分
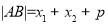
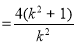 ,
,
点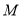 到直线
到直线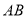 的距离为
的距离为 , 9分
, 9分
∴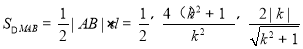
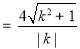
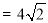 , 10分
, 10分
解得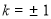 , 11分
, 11分
故直线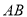 的方程为:
的方程为: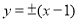 .即
.即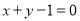 或
或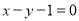 . 12分
. 12分
考点:1.抛物线的性质.2.直线与抛物线的关系.3.弦长公式,点到直线的距离.4.运算能力.


科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试文科数学试卷(解析版) 题型:选择题
执行右边的程序框图,若输入的 的值为–2,则输出
的值为–2,则输出 的值是( )
的值是( )
A. B.
B. C.
C. D.
D.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:选择题
在数列 中,
中, ,且
,且 ,
, ,若数列
,若数列 满足
满足 ,则数列
,则数列 是( )
是( )
A.递增数列 B.递减数列 C.常数列 D.摆动数列
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:选择题
观察下列关于两个变量 和
和 的三个散点图,它们从左到右的对应关系依次为( )
的三个散点图,它们从左到右的对应关系依次为( )

A.正相关、负相关、不相关 B.负相关、不相关、正相关
C.负相关、正相关、不相关 D.正相关、不相关、负相关
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查文科数学试卷(解析版) 题型:选择题
某几何体的三视图如右图所示,则该几何体的表面积是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练四(解析版) 题型:选择题
设数列{an}是等差数列,若a3+a4+a5=12,则a1+a2+…+a7=( )
A.14 B.21 C.28 D.35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com