
分析 构造bn=an+1-an,可判数列{bn}是4为首项2为公差的等差数列,累加法可得an=n(n+1),裂项相消法可得答案.
解答 解:构造bn=an+1-an,则b1=a2-a1=4,
由题意可得(an+2-an+1)-(an+1-an)=bn+1-bn=2,
故数列{bn}是4为首项2为公差的等差数列,
故bn=an+1-an=4+2(n-1)=2n+2,
故a2-a1=4,a3-a2=6,a4-a3=8,…,an-an-1=2n,
以上n-1个式子相加可得an-a1=$\frac{(n-1)(4+2n)}{2}$,解得an=n(n+1),
故$\frac{2016}{{a}_{1}}$+$\frac{2016}{{a}_{2}}$+…+$\frac{2016}{{a}_{2016}}$=2016($\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2016×2017}$)
=2016(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2016}$-$\frac{1}{2017}$)=2016-$\frac{2016}{2017}$,
∴[$\frac{2016}{{a}_{1}}$+$\frac{2016}{{a}_{2}}$+…+$\frac{2016}{{a}_{2016}}$]=2015,
故答案为:2015.
点评 本题考查等差数列的通项公式,涉及等差数列的判定和累加法以及裂项相消法求和,属中档题.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 | B. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 | ||
| C. | $\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1和$\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1或$\frac{9{x}^{2}}{4}$-$\frac{3{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $-\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
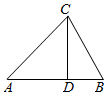 如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°.
如图,在△ABC中,|$\overrightarrow{CA}$|=$\sqrt{6}$,|$\overrightarrow{CB}$|=2,∠ACB=75°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两焦点与短轴的一个端点的连线构成等边三角形,直线x+y+2$\sqrt{2}$-1=0与以椭圆C的右焦点为圆心,椭圆的长半轴为半径的圆相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两焦点与短轴的一个端点的连线构成等边三角形,直线x+y+2$\sqrt{2}$-1=0与以椭圆C的右焦点为圆心,椭圆的长半轴为半径的圆相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com