
分析 由题意作出其平面区域,从而求出其面积,再由斜率的定义求得$\frac{7}{13}$≤$\frac{y}{x}$≤3,化简$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{x}{y}$+$\frac{y}{x}$,从而求其取值范围.
解答 解:由题意作出其平面区域,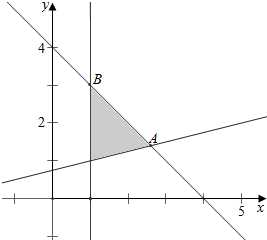
由题意可得,A($\frac{13}{5}$,$\frac{7}{5}$),B(1,3);
故点(x,y)对应的区域的面积S=$\frac{1}{2}$×2×($\frac{13}{5}$-1)=$\frac{8}{5}$
则$\frac{7}{13}$≤$\frac{y}{x}$≤3;
∵$\frac{{x}^{2}+{y}^{2}}{xy}$=$\frac{x}{y}$+$\frac{y}{x}$
∴2≤$\frac{x}{y}$+$\frac{y}{x}$≤$\frac{10}{3}$
故答案为:$\frac{8}{5}$,[2,$\frac{10}{3}$].
点评 本题考查了简单线性规划,作图要细致认真,用到了表达式的几何意义的转化,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
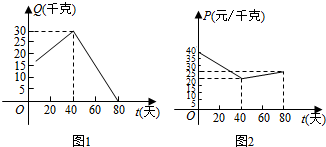
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
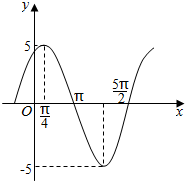 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,则函数的解析式为y=5sin($\frac{2}{3}$x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
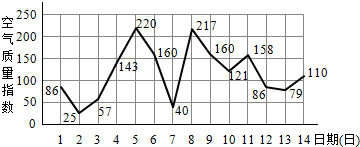 如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
如图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表,某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).| 空气质量指数 | 污染程度 |
| 小于100 | 优良 |
| 大于100且小于150 | 轻度 |
| 大于150且小于200 | 中度 |
| 大于200且小于300 | 重度 |
| 大于300且小于500 | 严重 |
| 大于500 | 爆表 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com