练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝loga(3－ax)．

    (1)当x∈[0,2]时，函数f(x)恒有意义，求实数a的取值范围；

    (2)是否存在这样的实数a，使得函数f(x)在区间[1,2]上为减函数，并且最大值为1？如果存在，试求出a的值；如果不存在，请说明理由．


     (1)由题意，3－ax>0对一切x∈[0,2]恒成立，∵a>0且a≠1，

    ∴g(x)＝3－ax在[0,2]上是减函数，从而g(2)＝3－2a>0得a<.∴a的取值范围为(0,1)∪.

    (2)假设存在这样的实数a，使得函数f(x)在区间[1,2]上为减函数，并且最大值为1.

    由题设f(1)＝1，即loga(3－a)＝1，

    ∴a＝，此时f(x)＝log，当x＝2时，函数f(x)没有意义，故这样的实数a不存在．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设二次函数f(x)＝ax2－2ax＋c在区间[0,1]上单调递减，且f(m)≤f(0)，则实数m的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝|2x－1|，a<b<c，且f(a)>f(c)>f(b)，则下列结论中，一定成立的是________．

    ①a<0，b<0，c<0;  ②a<0，b≥0，c>0；

    ③2－a<2c;  ④2a＋2c<2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若f(x)＝ax－，且f(lga)＝，则a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若logmn＝－1，则m＋3n的最小值是(　　)

    A．2                                                       B．2

    C．2                                                             D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝logax在[2，＋∞)上恒有|f(x)|>1，则(　　)

    A．0<a<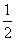或1<a<2                                      B．0<a<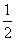或a>2

    C.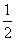<a<1或1<a<2                                        D.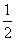<a<1或a>2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知x、y为正实数，则(　　)

    A．2lgx＋lgy＝2lgx＋2lgy                                     B．2lg(x＋y)＝2lgx·2lgy

    C．2lgx·lgy＝2lgx＋2lgy                                      D．2lg(xy)＝2lgx·2lgy

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知f(x)＝3x，并且f(a＋2)＝18，g(x)＝3ax－4x的定义域为[－1,1]．

    (1)求函数g(x)的解析式；

    (2)判断g(x)的单调性；

    (3)若方程g(x)＝m有解，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果函数f(x)＝x2＋bx＋c对任意的实数x都有f(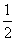＋x)＝f(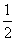－x)，那么(　　)

    A．f(－2)<f(0)<f(2)                                       B．f(0)<f(－2)<f(2)

    C．f(2)<f(0)<f(－2)                                       D．f(0)<f(2)<f(－2)

    查看答案和解析>>

    同步练习册答案