考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)通过讨论a的范围,从而求出函数的单调区间,
(Ⅱ)将问题转化为x
2-ax-4≤0在x∈(0,1]时恒成立,而函数
y=x-在区间(0,1]上是增函数,所以
y=x-的最大值为-3,从而求出a的范围.
解答:
解:(Ⅰ)函数f(x)的定义域(0,+∞),
f′(x)=1-=,
当a≤0时,f'(x)>0恒成立,此时,函数f(x)在(0,+∞)上是增函数;
当a>0时,由f'(x)>0解得x>a;由f'(x)<0解得0<x<a,
此时,函数f(x)在(a,+∞)上是增函数;f(x)在(0,a)上是减函数.
(Ⅱ)当a≤0时,函数f(x)在(0,1]上是增函数,
又函数
y=在(0,1]上是减函数,不妨设0<x
1<x
2≤1,
则
|f(x1)-f(x2)|=f(x2)-f(x1),|-|=-,
所以
|f(x1)-f(x2)|<4|-|等价于
f(x2)-f(x1)<-,
即
f(x2)+<f(x1)+.
设
h(x)=f(x)+=x-1-alnx+,
则
|f(x1)-f(x2)|<4|-|等价于函数h(x)在区间(0,1]上是减函数.
于是
h′(x)=1--=≤0即x
2-ax-4≤0在x∈(0,1]时恒成立,
从而
a≥x-在x∈(0,1]上恒成立,
而函数
y=x-在区间(0,1]上是增函数,所以
y=x-的最大值为-3.
于是a≥-3,又a<0,所以a∈[-3,0).
点评:本题考查了函数的单调性,函数的最值问题,考查导数的应用,求参数的范围,考查转化思想,是一道综合题.



 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案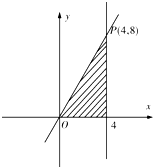 设不等式组
设不等式组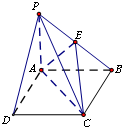 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4