
【题目】已知函数f(x)=ax﹣(a+2)lnx![]() 2,其中a∈R.
2,其中a∈R.
(1)当a=4时,求函数f(x)的极值;
(2)试讨论函数f(x)在(1,e)上的零点个数.
【答案】(1)极大值6ln2,极小值4;(2)分类讨论,详见解析.
【解析】
(1)把a=4代入后对函数求导,然后结合导数可求函数的单调性,进而可求极值;
(2)先对函数求导,然后结合导数与单调性关系对a进行分类讨论,确定导数符号,然后结合导数与函数的性质可求.
(1)当a=4时,f(x)=4x﹣6lnx![]() 2,
2,![]() ,x>0,
,x>0,
易得f(x)在(0,![]() ),(1,+∞)上单调递增,在(
),(1,+∞)上单调递增,在(![]() )上单调递减,
)上单调递减,
故当x![]() 时,函数取得极大值f(
时,函数取得极大值f(![]() )=6ln2,当x=1时,函数取得极小值f(1)=4,
)=6ln2,当x=1时,函数取得极小值f(1)=4,
(2)![]() ,
,
当a≤0时,f(x)在(1,e)上单调递减,f(x)<f(1)=a≤0,此时函数在(1,e)上没有零点;
当a≥2时,f(x)在(1,e)上单调递增,f(x)>f(1)=a≥2,此时函数在(1,e)上没有零点;
当0![]() 即
即![]() 时,f(x)在(1,e)上单调递减,由题意可得,
时,f(x)在(1,e)上单调递减,由题意可得, ,
,
解可得,0![]() ,
,
当![]() 即
即![]() 时,f(x)在(1,
时,f(x)在(1,![]() )上单调递减,在(
)上单调递减,在(![]() )上单调递增,
)上单调递增,
由于f(1)=a>0,f(e)=a(e﹣1)![]() ,
,
令g(a)=f(![]() )=2﹣(a+2)ln
)=2﹣(a+2)ln![]() a+2=(a+2)lna﹣(1+ln2)a+4﹣2ln2,
a+2=(a+2)lna﹣(1+ln2)a+4﹣2ln2,
令h(a)![]() ,则
,则![]() 0,
0,
所以h(a)在(![]() )上递减,h(a)>h(2)=1>0,即g′(a)>0,
)上递减,h(a)>h(2)=1>0,即g′(a)>0,
所以g(a)在(![]() )上递增,g(a)>g(
)上递增,g(a)>g(![]() )=2
)=2![]() ,
,
即f(![]() )>0,
)>0,
所以f(x)在(1,e)上没有零点,
综上,当0<a![]() 时,f(x)在(1,e)上有唯一零点,
时,f(x)在(1,e)上有唯一零点,
当a≤0或a![]() 时,f(x)在(1,e)上没有零点.
时,f(x)在(1,e)上没有零点.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:
【题目】为迎接“五一国际劳动节”,某商场规定购买超过6000元商品的顾客可以参与抽奖活动现有甲品牌和乙品牌的扫地机器人作为奖品,从这两种品牌的扫地机器人中各随机抽取6台检测它们充满电后的工作时长相关数据见下表(工作时长单位:分)
机器序号 | 1 | 2 | 3 | 4 | 5 | 6 |
甲品牌工作时长/分 | 220 | 180 | 210 | 220 | 200 | 230 |
乙品牌工作时长/分 | 200 | 190 | 240 | 230 | 220 | 210 |
(1)根据所提供的数据,计算抽取的甲品牌的扫地机器人充满电后工作时长的平均数与方差;
(2)从乙品牌被抽取的6台扫地机器人中随机抽出3台扫地机器人,记抽出的扫地机器人充满电后工作时长不低于220分钟的台数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的右顶点为
的右顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线与
的直线与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于另一个点
交于另一个点![]() ,且点
,且点![]() 在
在![]() 轴上的射影恰好为点
轴上的射影恰好为点![]() .
.
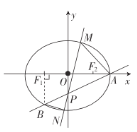
(1)求点![]() 的坐标;
的坐标;
(2)过点![]() 且斜率大于
且斜率大于![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点
两点![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,![]() )的最小正周期为π,且关于
)的最小正周期为π,且关于![]() 中心对称,则下列结论正确的是( )
中心对称,则下列结论正确的是( )
A.f(1)<f(0)<f(2)B.f(0)<f(2)<f(1)
C.f(2)<f(0)<f(1)D.f(2)<f(1)<f(0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() 两点.
两点.
(1)若![]() 过点
过点![]() ,且
,且![]() ,求
,求![]() 的斜率;
的斜率;
(2)若![]() ,且
,且![]() 的斜率为
的斜率为![]() ,当
,当![]() 时,求
时,求![]() 在
在![]() 轴上的截距的取值范围(用
轴上的截距的取值范围(用![]() 表示),并证明
表示),并证明![]() 的平分线始终与
的平分线始终与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足
满足![]() ,数列
,数列![]() 为
为![]() 数列,记
数列,记![]() .
.
(1)写出一个满足![]() ,且
,且![]() 的
的![]() 数列
数列![]() ;
;
(2)若![]() ,
,![]() ,证明:
,证明:![]() 数列
数列![]() 是递增数列的充要条件是
是递增数列的充要条件是![]() ;
;
(3)对任意给定的整数![]() ,是否存在首项为0的
,是否存在首项为0的![]() 数列
数列![]() ,使得
,使得![]() ?如果存在,写出一个满足条件的
?如果存在,写出一个满足条件的![]() 数列
数列![]() ;如果不存在,说明理由.
;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】赵爽是我国汉代数学家、天文学家,他在注解《周髀算经》时,介绍了“勾股圆方图”,亦称“赵爽弦图”,它被2002年国际数学家大会选定为会徽.“赵爽弦图”是以弦为边长得到的正方形,该正方形由4个全等的直角三角形加上中间一个小正方形组成类比“赵爽弦图”,可类似地构造如图所示的图形它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形设DF=2AF=2,若在大等边三角形中随机取一点,则此点取自三个全等三角形(阴影部分)的概率是( )
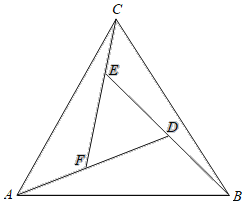
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com