
分析 (1)原不等式可化为:|x-1|>1-x2,即x-1>1-x2或x-1<x2-1,即可求不等式f(x)+x2-1>0的解集;
(2)原不等式等价于|x-1|+|x+3|<m的解集非空,令h(x)=|x-1|+|x+3|,即h(x)min<m,即可求实数m的取值范围.
解答 解:(1)原不等式可化为:|x-1|>1-x2,即x-1>1-x2或x-1<x2-1,
由x-1>1-x2,得x>1或x<-2;由x-1<x2-1,得x>1或x<0.
综上,原不等式的解集为{x|x>1或x<0}.
(2)原不等式等价于|x-1|+|x+3|<m的解集非空,
令h(x)=|x-1|+|x+3|,即h(x)min<m,
由|x-1|+|x+3|≥|x-1-x-3|=4,所以h(x)min=4,所以m>4.
点评 本题考查不等式的解法,考查函数的最值,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
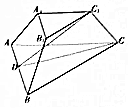 已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.
已知三棱台ABC-A1B1C1中,AB=BC=4,AC=2A1C1=2$\sqrt{2}$,AA1=CC1=1,平面AA1B1B⊥平面AA1C1C.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p:?x0∈R,x02-x0+1<0,则¬p:?x∉R,x2-x+1≥0 | |
| B. | 已知相关变量(x,y)满足回归方程$\stackrel{∧}{y}$=2-4x,若变量x增加一个单位,则y平均增加4个单位 | |
| C. | 命题“若圆C:(x-m+1)2+(y-m)2=1与两坐标轴都有公共点,则实数m∈[0,1]为真命题 | |
| D. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\;\frac{1}{3})$ | B. | $(\frac{1}{3},\;\frac{1}{2})$ | C. | $(\frac{1}{2},\;\frac{2}{3})$ | D. | $(\frac{2}{3},\;1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,3] | B. | (-∞,-3]∪[3,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | [-1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com