
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为![]() .
.
(1)写出曲线C1和C2的直角坐标方程;
(2)已知P为曲线C2上的动点,过点P作曲线C1的切线,切点为A,求|PA|的最大值.
【答案】(1)C1的直角坐标方程为![]() ;C2的直角坐标方程为
;C2的直角坐标方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() ,可得曲线C1的直角坐标方程.由
,可得曲线C1的直角坐标方程.由![]() ,得ρ2+3ρ2sin2θ=4,结合极坐标与直角坐标的互化公式可得曲线C2的直角坐标方程;
,得ρ2+3ρ2sin2θ=4,结合极坐标与直角坐标的互化公式可得曲线C2的直角坐标方程;
(2)由P为曲线C2上的动点,设P(2cosα,sinα),则P与圆的圆心的距离![]() ,利用二次函数求最值,再由勾股定理求|PA|的最大值.
,利用二次函数求最值,再由勾股定理求|PA|的最大值.
解:(1)由![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() ,可得
,可得![]() .
.
∴曲线C1的直角坐标方程为![]() ;
;
由![]() ,得ρ2+3ρ2sin2θ=4,
,得ρ2+3ρ2sin2θ=4,
即x2+y2+3y2=4,即![]() .
.
∴曲线C2的直角坐标方程为![]() ;
;
(2)∵P为曲线C2上的动点,又曲线C2的参数方程为![]()
∴设P(2cosα,sinα),
则P与圆C1的圆心的距离
 .
.
要使|PA|的最大值,则d最大,当sinα![]() 时,d有最大值为
时,d有最大值为![]() .
.
∴|PA|的最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2020年是我国垃圾分类逐步凸显效果关键的一年.在国家高度重视,重拳出击的前提下,高强度、高频率的宣传教育能有效缩短我国生活垃圾分类走入世界前列所需的时间,打好垃圾分类这场“持久战”,“全民战”.某市做了一项调查,在一所城市中学和一所县城中学随机各抽取15名学生,对垃圾分类知识进行问答,满分为100分,他们所得成绩如下:
城市中学学生成绩分别为:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
县城中学学生成绩分别为:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根据上述两组数据在图中完成两所中学学生成绩的茎叶图,并通过茎叶图比较两所中学学生成绩的平均分及分散程度;(不要求计算出具体值,给出结论即可)
(2)记这30名学生成绩80分以上为良好,80分以下为一般,完善表格,并判断是否有99%的把握认为该城市中学和县城中学的学生在了解垃圾分类知识上有差异?(结果保留三位小数)
学生成绩 | 良好 | 一般 | 合计 |
城市中学学生 | |||
县城中学学生 | |||
合计 |
附: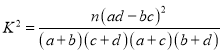 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】菱形![]() 中,
中,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
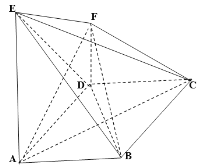
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() 使得直线
使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求
?若存在,求![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,离心率为
,离心率为![]() ,
,![]() 是椭圆上的一个动点(不与左、右顶点重合),且
是椭圆上的一个动点(不与左、右顶点重合),且![]() 的周长为6,点
的周长为6,点![]() 关于原点的对称点为
关于原点的对称点为![]() ,直线
,直线![]() 交于点
交于点![]() .
.
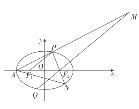
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于另一点
与椭圆交于另一点![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线C:![]() 1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若
1(a>0,b>0)右焦点F2作双曲线一条渐近线的垂线,垂足为P,与双曲线交于点A,若![]() ,则双曲线C的渐近线方程为( )
,则双曲线C的渐近线方程为( )
A.y=±![]() xB.y=±xC.y=±2xD.y=±
xB.y=±xC.y=±2xD.y=±![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 中,
中,![]() 与
与![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() 平面
平面![]() .
.
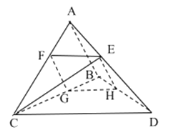
(1)求证:![]() ;
;
(2)过![]() 作一平面分别交
作一平面分别交![]() ,
, ![]() ,
, ![]() 于
于![]() ,
,![]() ,
,![]() ,若四边形
,若四边形![]() 为平行四边形,求多面体
为平行四边形,求多面体![]() 的表面积.
的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com